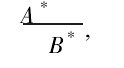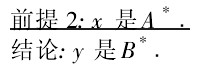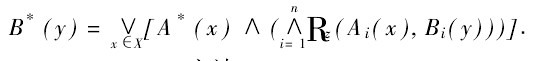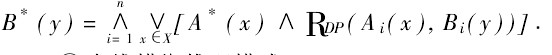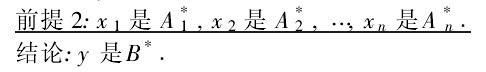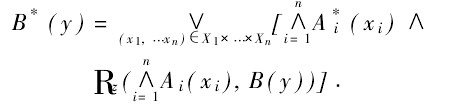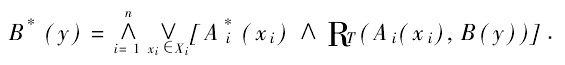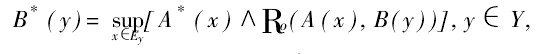模糊推理

出自 MBA智库百科(https://wiki.mbalib.com/)

　　模糊推理作为近似推理的一个分支,是模糊控制的理论基础。在实际应用中,它以数值计算而不是以符号推演为特征,它并不注重如像经典逻辑那样的基于公理的形式推演或基于赋值的语义运算,而是通过模糊推理的算法,由推理的前提计算出(而不是推演出)结论。1973年,Zadeh首先给出了模糊推理理论中最基本的推理规则即模糊分离规则FMP(fuzzy modus ponens)^[2],随后被Zadeh和Mamdani等人算法化^[3][4],形成了当今以推理合成规则CRI(compositional rule of inference)为主要基础的各种模糊推理方法;但是王国俊近年认为模糊推理算法以CRI为基础存在缺陷,并提出了一种完全基于蕴涵算子的3I算法^[5]。30余年来,模糊推理方法在工业生产控制、特别是在家电产品中的成功应用,使得它们在模糊系统以及自动控制等领域愈来愈受到人们的重视,如今在近似推理中已成为以数值计算而不是以符号推演为特征的一个研究发展方向。

　　然而,尽管这些基于Zadeh与Mamdani等人的工作而发展的各种模糊推理算法用于经验控制领域比其他方法有效,但从本质上不难看出实用中的模糊控制与逻辑控制的关联越来越少,而对算法的依赖却越来越多^[6]。因此,用算法代替模糊推理在理论上是否合理,其算法的理论基础是否可靠仍被人置疑,如Elkan在1994年国际人工智能大会上所作的颇有影响的“模糊逻辑的似是而非的成功”的报告^[7]。

　　我们知道,在推理系统中,一个结论是由前提通过逻辑推理而得出的结果,但模糊推理算法实质上是通过人为规定的方法计算出结果而不是推理出逻辑结论,具体就是将推理前提约定为一些算子,再借助于一些运算计算出结论,可见模糊推理算法虽实用但主观性强,本身的理论基础贫弱。因此,将模糊推理算法作为研究对象,从理论上对模糊推理算法的构造基础进行分析研究,论证用计算去替代模糊推理的算法的理论依据是重要的。

　　1)模糊推理最基本的模式为模糊假言推理FMP(fuzzy modus ponens)^[8][9],其格式如下一般格式:。

　　前提1:若x是A,则y是B

　　模糊推理公式.jpg

　　形式化表示:

　　A→B

　　这里,A,A ^* 是论域X上的模糊集,B,B ^* 是论域Y上的模糊集·1973年Zadeh提出著名的CRI(compositionalrule of inference)算法·具体是,首先定义蕴涵算子。

　　利用R_z把前提1中的A→B转换为X×Y上一个模糊关系R(x,y):

　　然后,将前提2中A^*与R通过合成运算得到B^*,即

　　。

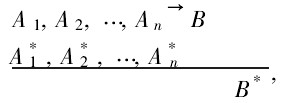
　　在模糊推理应用中,对于FMP,还有诸如Baldwin算法、Mizumoto算法等·但迄今为止,CRI算法还是最基本、最重要的方法[4,6,10]·2)除了FMP外,模糊推理中还有多重(多条规则)模糊推理mcFMP(multiple conditional fuzzy modusponens)和多维模糊推理mdFMP(multidimensionalfuzzy modus ponens),其格式及典型算法[6]如下(限于篇幅,分别只列举2种算法):。

　　①多重模糊推理模式mcFMP

　　一般格式:

　　前提1:若x是A₁,则y是B₁,

　　　　　若x是A₂,则y是B₂,

　　　　　┇

　　　　　若x是A_n,则y是B_n

　　形式化格式

　　其中,A_i,A ^* 是论域X上的模糊集,B_i,B ^* 是论域Y上的模糊集,i=1,2,…,n,n≥2。

　　Zadeh算法：

　　Dubois-Prade方法:

　　②多维模糊推理模式mdFMP

　　一般格式:

　　前提1:若x₁是A₁,x₂是是A_n,则。

　　y是B·

　　形式化格式:

　　其中,是论域X_i上的模糊集,B,B ^* 是论域Y上的模糊集,i=1,2,…,n。

　　Zadeh算法:

　　Tsukamoto算法:

　　R_T = R_z

　　从上述不难看出,对于多重模糊推理mcFMP以及多维模糊推理mdFMP,它们的算法都是基于CRI的,所不同的是在算法中采用了两种途径·第1种途径是先把前提1中的n条规则聚合为一个模糊关系,然后再与前提2中的A ^* (或者进行合成(composition)求得B ^* ,如①,②中的Zadeh算法;第2种途径则是先将前提2中的A ^* (或)分别与前提1中的n条规则合成得到n个模糊关系,然后再进行合成求得B ^* ,如①中Dubois-Prade算法和②中Tsukamoto算法·30年来,虽然有不少学者提出过不同于CRI的模糊推理算法,CRI算法本身也有各种变形和发展,但实用中的大多数模糊推理算法仍以CRI算法的思想为基础·然而,对于CRI算法在将前提中的蕴涵关系转化为模糊关系时使用了一次能体现推理思想的蕴涵算子后,就直接借助于合成运算给出推理结果,王国俊近年认为是一缺陷并提出了一种完全基于蕴涵算子的3I算法[4,10,13],即重新建立一个蕴涵算子R_e,在3I原则(认为FMP应该是三重蕴涵关系下,提出R_e型3I算法:

　　R_e(a,b),,当a≤b；否则,

　　其中

　　3I算法虽然没有在应用中检验,但它是一个不使用合成运算而采用三重模糊蕴涵关系的非CRI算法,理论上具有一些良好特性,使得模糊推理算法更具逻辑推理的特征。

　　从逻辑推理的本质来说,模糊逻辑与一般逻辑系统应具有相同的推理特征,既从一组前提出发推导出结论P的演绎是由逻辑系统的推理规则(公理也可作为推理规则)支配的,所不同的是,在模糊逻辑中前提和结论均允许是模糊命题。所谓模糊推理就是一种由具有模糊性的前提推导出结论的逻辑过程,因此,模糊推理由前提推导出模糊结论的准确程度,关键在于对前提1与前提2置以什么样的(模糊)关系结构,以及前提条件与结论又置以什么样的(模糊)关系结构。

　　对如上模糊推理算法的思想以及构造进行分析,我们认为

　　1)算法的基本思想就是把推理模式中用词语描述的一组推理规则转换成描述中变项之间的一种模糊关系,从而使模糊推理过程的实现都基于模糊关系。据此,可认为模糊推理算法实质上是模糊推理的变换成的模糊关系的算法。对具体算法来说,无论是CRI算法(以及以CRI为基础的各种算法)还是3I算法,首先都遵循CRI算法的第一步即利用蕴涵算子,把已知前提1中的A→B转化为X×Y上一个模糊关系R(x,y)。然后,Zadeh的思想是将FMP中所求的B*看做是以A→B和A ^* 为前提而推导的结论,即形式关系为A ^* ＆ ,这一点是符合一般逻辑的推理规则的;3I算法的思想是将FMP中所求的B*看做是在以A→B为前提下由A ^* 推导出来的,即形式关系为。对于这两种关于FMP推理意义的理解,若A ^* ＆为,则从逻辑语形的角度看,与是等同的,但是若从逻辑语义的角度看,前者比后者更符合FMP的推理涵义。然而,Zadeh在CRI算法中却将前提2与前提1之间的关系用复合运算刻画,这一点是缺乏根据的,并且致使CRI算法失去应有的推理涵义。相比之下,思想基于FMP的形式推理结构为的3I算法,避免了CRI算法的缺陷并具有许多良好性质·但是,在3I算法中,结论B ^* (y)(B ^* 的隶属度)的表达式从何而来,其中为什么具有与CRI算法相同的关系结构。

　　2)从算法的结构看,模糊推理的各种算法虽然各自采用的蕴涵算子不同,但由于模糊蕴涵算子是[0,1]×[0,1]到[0,1]上的映射,模糊蕴涵可由代表模糊“与”、模糊“或”、模糊“非”的3个基础算子t∧(t-模)、t∨(t-余模)以及t^c(补)构造出来,并且,各种模糊推理算法中求解B ^* (y)的表达式也以t-模、t-余模和补t^c为基础算子,由此我们认为,除了针对mcFMP和mdFMP而提出的引进距离或贴近度等概念的算法[4,10]外,诸如上述的模糊推理的各种经典算法计算出的结论,实际上是由前提条件通过t∧,t∨和t^c三个基础算子在[0,1]上进行运算得出的结果,对模糊推理采用计算的算法其本质上是对计算对象(推理前提)运用基础算子进行运算的方法,因此,通过这种方法计算得到的结果与计算对象之间就应存在某一数学关系。对此,我们得到如下结果。