概率論模型
出自 MBA智库百科(https://wiki.mbalib.com/)
- 概率論模型(Probabilistic Model)
目錄 |
什麼是概率論模型[1]
概率論模型是基於概率排序原理,在概率框架中處理信息檢索問題。模型中假設特征項之間是相互獨立的,該模型是基於概率原則:給定一個用戶查詢q和文檔集中的一個文檔dj,概率模型試圖估計用戶找到其感興趣的文檔dj的概率,概率模型假設這個相關概率只是依賴於查詢和文檔表示。進而假設模型在文檔集中存在一個子集,它是查詢q的結果集。理想結果集記為R,它使得總體的相關概率最大。集合R中的文檔被認為是與查詢相關的,不在集合R中的文檔則被認為是不相關的。
概率論模型基本上是一種基於貝葉斯決策理論的自適應模型。與前兩種模型不同的是,它的查詢式子不是直接由用戶編定的。而是由系統通過某種歸納式學習過程(相關反饋)來構造一個決策函數去表示信息查詢。
概率論模型的基礎[2]
概率論模型的基礎是概率,預估計信息資源與用戶需求的相關性,根據相關性大小進行排序,排到最前面的文檔將會是最有可能滿足用戶需求的文檔。Van Rijsbergen和Robertson等人提出的概率檢索模型的基本思想是根據先前檢索過程中得到的相關性先驗信息來計算文檔集合中每篇文檔成為相關文檔的概率,並根據統計理論(如貝葉斯決策等)來確定哪些文檔可作為輸出文檔集。相關工作中,將布爾檢索和概率檢索模型有機地結合起來,但它在沒有獲得樣本文檔之前,無法估計詞條相關性且該方法複雜度較大。
概率論模型的基本準則[3]
概率論模型的基本準則是:文本按照與查詢的概率相關性大小排序,排在前面的文本是最有可能被獲取的文本,即如果文本滿足如下公式則該文本被獲取:
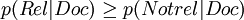
其中,p(Rel | Doc)表示文本Doc與查詢有關的條件概率;p(Notrel | Doc)表示文本Doc與查詢不相關的條件概率。根據貝葉斯規則,上述公式可以改寫成
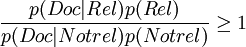
所獲取的文本可以利用上述公式的左端進行排序。
利用概率論模型的關鍵是如何計算左端式子中的概率。如果查詢由一個片語成,或者組成查詢的詞之間相互獨立,那麼查詢詞的權重可以由下式計算:
![w=\frac{r/(R-r)}{(n-r)/[N-n-(R-r)]}](/w/images/math/3/6/9/3699b421eacbfce64b9e490436e4c819.png)
式中,N是文本庫中文本的數量;n是文本庫中包含該詞的文本數量;R是與查詢相關的文本數目(相關的文本數目在訓練文本庫中是已知的);r是與查詢相關而且包含該詞的文本數目。
這樣查詢q可以表示為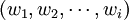 ,其中,叫wi由上述公式計算得到。文本d表示為
,其中,叫wi由上述公式計算得到。文本d表示為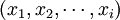 ,其中,如果詞存在於文本中,則對應的xi = 1,反之則xi = 0。查詢q與文本d之間的相似度函數定義為
,其中,如果詞存在於文本中,則對應的xi = 1,反之則xi = 0。查詢q與文本d之間的相似度函數定義為
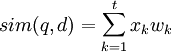
利用概率論模型的典型系統有Kwok與Robertson等,它們在利用樣本計算詞權重的過程中考慮了詞在文檔中出現的頻率,其中Kwok系統還考慮了詞在整個樣本集合中出現的頻率。概率論模型的效果要明顯優於布爾模型,但比向量空間模型略差。
概率論模型的一個特例是貝葉斯網路,由於該模型適合於超文本系統,因此在超文本信息成為當前信息獲取主流信息的情況下,該模型的應用越來越廣泛。







