概率盤法

出自 MBA智库百科(https://wiki.mbalib.com/)

概率盤法(The Probability Wheel)

　　概率盤法是由美國斯坦福大學教授霍瓦德(Howzud)提出的，這種方法具體是，先制一個圓盤，這一圓盤稱為概率盤，圓盤被劃分為兩個扇形區，分別塗上兩種不同的顏色，如橙色和藍色，如圖所示，兩個扇形的面積可任意調整，且圓盤的反面有刻度，圓盤正面的橙色區則是反面的藍色區，由反面的刻度可查得正面的橙色區所占整個圓盤面積的百分比。設事件發生在圓盤任何相同面積扇形區中的可能性是相等的，圓盤調整結束後，查圓盤反面的刻度就知道一事件發生在橙色區中的概率。概率盤法實質上是試圖通過調整圓盤中橙色區的大小。最終使決策者認為某一事件發生的概率與橙色區面積的百分比一致為止，然後通過查反面的對應刻度就能獲得決策者對該事件發生概率的主觀估計，決策者若對狀態空間B中的所有狀態(最多可允許一個狀態不試驗)均按此方法求其主觀估計概率，那麼，狀態空間B的概率分佈也就可以近似地求得。

　　用概率盤測定未知事件發生的概率的過程是這樣的。它基於對被測人進行兩種賭博式的詢問，一種是針對某一未知事件發生概率的推測，另一種是對概率盤的指針落在黑色區域的推測。然後詢問決策人，這兩種推測中哪一種更可能發生。如果決策人認為其中一種推測比另一種推測更可能發生，則調整概率盤上黑色區域大小，再次詢問決策人，直到決策人認為這兩種推測有相等的可能性時為止。這時，從概率盤上求出黑色區域占總面積的比率，這個比率就是未知事件可能發生的概率。

　　例如，某公司的利潤和原油價格有較大關係，現想預計今後五年中，原油價格漲、低、平穩的概率。假定現在的價格是30元欄，且設五年內不會有石油禁運發生。為了獲得這一主觀概率，決策人詢問一個石油經銷商。

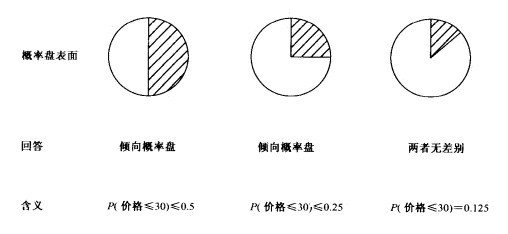
　　首先把概率盤上的黑白區域調整為相等，然後問被測人，是願意打賭——“概率盤上的指針落在黑色區域”，還是打賭——“在五年內石油的價格低於30元”。假定被測人認為概率盤上的指針落在黑色區的可能性大，(也就是說他願意在概率盤上打賭)。那麼決策人把黑色區縮小，比如縮到1／4面積，再詢問被測人，在這種情況下，他願意打哪一個賭——是概率盤上的指針落在黑色區域上的賭，還是認為五年內石油價格低於30元。

　　如果被測人仍認為指針落在黑色區(現為1／4圓盤面積)的可能性大。則再縮小黑色區，比如1／8圓盤面積，再問被測人。這一回被測人可能會說：“好了，我現在既不願意在概率盤上賭搏，也不願意賭石油價格在五年內會在30元以下，我覺得這兩種賭博有相同的結果。”

　　這樣我們就可認為石油價格低於30元的概率是0．125(1／8圓盤的面積)。上面的詢問過程可用下圖表示。下一步再提出一個新的問題。

　　如石油價格是否會高於32元，進行與上面相同的詢問。假定石油價格高於32元的推測與概率盤黑色區域占1／2的可能性相等，這時可認為價格高於32元的概率是0．5。

　　那麼價格在30—32元之間的可能性就是1 - 0．5 - 0．125=0．375。

　　當然還可以對這最後的結論進行檢查，也就是將概率撤十的黑色區調整為整個面積為0．375，然後問被測人，他是否認為指針落在黑色區域的可能性，與石油價格在30—32元的可能性相等。如果被測人認為是相等的，則試驗中止，如認為是不等的，則要從頭開始，重覆以前的試驗，以便找出不相吻合的原因。

　　如果測出的概率總和不等於1，但很接近，這時可以把數據正常化，即把每個預測值被總和除，得到概率值。