時域均衡

出自 MBA智库百科(https://wiki.mbalib.com/)

　　實際的基帶傳輸系統不可能完全滿足無碼間串擾傳輸條件，因的基帶傳輸系擾是不可避免的。當串擾嚴重時，必須對系統的傳輸函數H（w）進行校正，使其達到或接近無碼間串擾要求的特性。理論和實踐表明，在基帶系統中插入一種可調（或不可調）濾波器就可以補償整個系統的幅頻和相頻特性，從而減小碼間串擾的影響。這個對系統校正的過程稱為均衡，實現均衡的濾波器稱為均衡器。

　　均衡分為頻域均衡和時域均衡。頻域均衡是從頻率響應考慮，使包括均衡器在內的整個系統的總傳輸函數滿足無失真傳輸條件。時域均衡是指直接從時間響應考慮，使包括均衡器在內的整個系統的衝激響應滿足無碼間串擾條件。

　　頻域均衡在通道特性不變，且傳輸低速率數據時是適用的，而時域均衡可以根據通道特性的變化進行調整，能夠有效地減小碼間串擾，故在高速數據傳輸中得以廣泛應用。

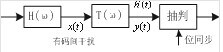
　　時域均衡的基本思想可用下圖所示的傳輸模型來簡單說明。

　　圖1中，H（w） 不滿足式的無碼間串擾條件時，其輸出信號 x(t)將存在碼間串擾。為此，在H(w)後插入一個稱之為橫向濾波器的可調濾波器T(w)，形成新的總傳輸函數H(w)，表示為H(w)=H(w)T(w)

　　顯然，只要 滿足式H(w)，即

　　則抽樣判決器輸入端的信號 y(t)將不含碼間串擾，即這個包含T(w)在內的H'(w)將可消除碼間串擾。這就是時域均衡的基本思想。

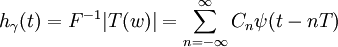
　　由上式可見， Cn、 T(w)完全由H(w)決定。

　　根據該式，可構造實現T（w）的插入濾波器如圖2所示，它實際上是由無限多個橫向排列的延遲單元構成的抽頭延遲線加上一些可變增益放大器組成，因此稱為橫向濾波器。每個延遲單元的延遲時間等於碼元寬度T(b)，每個抽頭的輸出經可變增益（增益可正可負）放大器加權後輸出。這樣，當有碼間串擾的波形x(t)輸入時，經橫向濾波器變換，相加器將輸出無碼間串擾波形 y(t)。

　　上述分析表明，藉助橫向濾波器實現均衡是可能的，並且只要用無限長的橫向濾波器，就能做到消除碼間串擾的影響。然而，使橫向濾波器的抽頭無限多是不現實的，大多情況下也是不必要的。因為實際通道往往僅是一個碼元脈衝波形對鄰近的少數幾個碼元產生串擾，故實際上只要有一、二十個抽頭的濾波器就可以了。抽頭數太多會給製造和使用都帶來困難。