拉奧—夏昆模型
出自 MBA智库百科(https://wiki.mbalib.com/)
目錄 |
拉奧(Ambar G.Rao)和夏昆(Melvin F.Shakun)於1972年提出了關於新品牌進入市場的價格模型。
拉奧—夏昆模型既充分考慮到了市場結構,又考慮到了在實現價格戰略過程中的企業品牌目標和競爭者目標。
拉奧—夏昆模型是建立在如下假設基礎上的:
(1)僅考慮同質顧客群體;
(2)顧客群體中某一成員願意支付的最低價格為呈對數正態分佈的隨機變數,且均值為μ,方差為δ2;
(3)對每一顧客來說,存在一固定的對數價格尺度,其間距為α,它標志著顧客可接受價格的幅度,顧客群體中某一成員願意支付的最大高價格也是對數正態分佈的隨機變數,且均值為(μ+α),方差為δ2。
單一品牌的最優價格公式:

為研究多品牌市場上有消費者選擇行為,拉奧和夏昆又引入了另外的行為假設,主要強調兩點:
(1)註重產品質量的顧客群體,占所有顧客的比例為λ,他們在可接受的價格幅度內願意購買較高價格的品牌;
(2)註重產品價格的顧客群體,占所有顧客的比例為(1-λ),在其可接受的幅度內願意購買較低價格的品牌。
通過推導可以得出結論:
(1)占所有顧客比例為πj的人不會轉向品牌2,因為他們認為P2是個太高的價格,這個比例也就是品牌忠誠細分市場,而
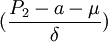
(2)如果P1-P2≥a,則這兩個品牌不構成競爭關係,因為它們並不分享同一市場上的購買者,在這種情況下,企業可通過市場結構分析,來決定是否引入新品牌來補充現有的品牌系列。
(3)品牌1可通過強調其產品質量而奪走品牌2的某些份額,這是λ值下降的結果,品牌2也可因強調其價廉而奪走品牌1的某些生意。
(4)品牌i的市場占有率Si為:
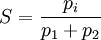
i=1,2
假定品牌1已占據市場而品牌2試圖進入市場。
在競爭條件下的結果是:
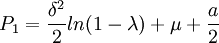
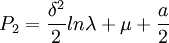
而當企業採取合作戰略(即第三種品牌定價目標)時,市場銷售最大化的最優價格分別為
P1=a
P2=μ+a







