折半平均法
用手机看条目
出自 MBA智库百科(https://wiki.mbalib.com/)
折半平均法(Semi-average Method)
目錄 |
[編輯]
什麼是折半平均法[1]
折半平均法也稱半數平均法，是指以數列前半部的平均數和後半部的平均數作為商個標準點，並以此兩點為依據，決定其趨勢直線。
[編輯]
折半平均法的應用[1]
採用這種方法的重要問題，是如何確定前後兩個部分中點的位置。
1.如原數列的項致為偶數，前後兩半數部分的中點，可依確定中位數位置的方法求得。
前半部中點的位置是：
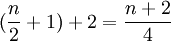
後半部中點的位置是：
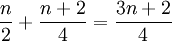
式中，n為原數列的項數
2.如原數列的項數為奇數，用捨去中項法。即將原數列的中間一項捨去，其餘前後兩半仍成偶數，分別求前半部和後半部的中點位置，可參照偶數項求中點的方法求得，但應該用(n-1)代替n。
前半部中點的位置是：
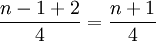
後半部中點的位置是：
[編輯]
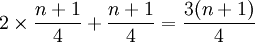
折半平均法與兩端平均法的區別[1]
兩端平均法與半數平均法的趨勢直線是不同的。兩端平均法的趨勢直線，因為只考慮兩端的數值，所以恰當地選擇平均數的時期是很重要的。如果代表兩端平均數的中點恰好在波底，則其趨勢直線必將偏低；如果代表兩端平均數的中點恰好選在浪尖，則其趨勢直線必將偏高。比較恰當的方法，是首末兩端平均數的中點，都選在波浪的中間位置，力求使趨勢直線符合實際情況。半數平均法，因為考慮到整個數列兩個部分的所有數值。所以其趨勢直線比較切合實際。
[編輯]
[編輯]
