成本分析模式
出自 MBA智库百科(https://wiki.mbalib.com/)
成本分析模式(Cost Analysis Model)
目錄 |
成本分析模式是根據現金有關成本,分析預測其總成本最低時現金持有量的一種方法。運用成本分析模式確定現金最佳持有量時,只考慮因持有一定量的現金而產生的機會成本及短缺成本,而不予考慮管理費用和轉換成本。這種模式下,最佳現金持有量,就是持有現金而產生的機會成本與短缺成本之和最小時的現金持有量。
(1)機會成本。企業由於持有一定數量的現金,必然放棄將其用於其他投資機會而可能獲得的收益,這種放棄的潛在收益就是持有現金的機會成本,一般可用企業的資本成本、資本收益率、證券投資收益率等指標來表示。機會成本與企業的現金持有量成正比,即現金持有量越大,機會成本越高。
(2)管理成本。企業持有現金會發生一些管理費用,如管理人員的工資、安全措施費用等這些費用就是現金的管理成本。管理成本是一種固定成本,它與現金持有量之間沒有明顯的變化關係。
(3)短缺成本。短缺成本是指企業由於現金持有量的不足,不能滿足正常的業務開支,使企業蒙受的損失或為此付出的代價,如喪失購買能力成本、信用損失成本等。短缺成本與現金持有量成反比,即現金持有量越大,短缺成本越低。
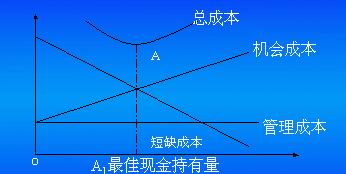
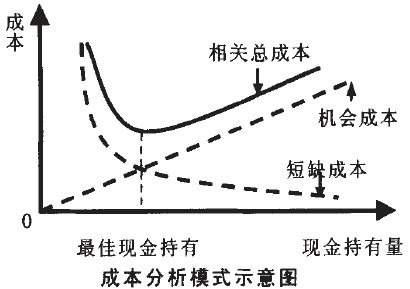
最佳現金持有量的成本分析模型,就是對以上兩種持有現金的相關成本進行分析,尋找使兩種成本總額最低的現金持有量。如果我們能夠找出相關成本與現金持有量之間的函數關係,則可以用坐標圖的方法來求解最佳的現金持有量。如圖所示,此時,相關總成本是一條凹形曲線,曲線的最低點即是持有現金相關總成本的最低點,相應的持有現金量就是最佳現金持有量C * 。
成本分析模型的優點是易於理解,但要求能夠確定決策相關成本與現金持有量的函數關係。通常情況下,企業可以根據機會成本與短缺成本相等條件下的現金持有量的原理,考察不同現金持有方案的機會成本與短缺成本,當兩種成本相等或者比較接近時的現金持有方案值得選擇。
案例一:運用成本分析模式確定某企業最佳現金持有量[1]
一、某企業概況
某企業現有ABCD四種現金持有方案,有關成本資料相關總成本最低,因此,企業選擇持有300,000元現金,即如下表。
現金持有量備選方案表
| 項目 | A | B | C | D |
| 現金持有量 | 100,000 | 200,000 | 300,000 | 400,000 |
| 機會成本率 | l0% | l0% | 10% | l0% |
| 短缺成本 | 48,000 | 25,000 | 10,000 | 5,000 |
根據上表採用成本分析模式編製該企業最佳現金持有量測算表數據如下表。
最佳現金持有量測算表
| 方案及現金持有量 | 機會成本 | 短缺成本 | 相關總成本 |
| A(100000) | 10,000 | 48,000 | 58,000 |
| B(200000) | 20,000 | 25,000 | 45,000 |
| C(300000) | 30,000 | 10,000 | 40,000 |
| D(400000) | 40,000 | 5,000 | 45,000 |
通過比較分析上表中各方案的總成本,由於C方案的相關總成本最低,因此,企業選擇持有300,000元現金,即最佳現金持有量為300,000元。
在採用成本分析模式確定最佳現金持有量時所共用,筆者以為這一思路本身並沒有什麼太大問題,只是在採用數據進行過程分析時,數據設計有違數理及成本分析模式本身的內在規定,應該重新進行數據設計,以使其更加合理。
二、現金相關總成本最低時機會成本與短缺成本關係的一點看法
採用成本分析模式確定最佳現金持有量時只考慮因持有一定量的現金而產生的機會成本及短缺成本,其他相關成本忽略不計。由於機會成本和現金持有量呈正相關,而短缺成本與現金持有量呈負相關,所以,由二者構成的相關總成本具有最小值,並且當且僅當二者相等時才取最小值。下麵筆者運用圖示法和數理法分別推導這一思路。
(1)圖示法下圖為現金的成本同現金持有量之間的關係圖。
從上圖可以看出,由於各項成本同現金持有量的變動關係不同,使得總成本曲線呈拋物線型,拋物線的最低點即為成本最低點,該點所對應的現金持有量便是最佳現金持有量,此時,機會成本曲線和短缺成本曲線相交,二者取值相等。
(2)數理法.在本部分我試運用數理的方法說明成本分析模式下何時現金持有相關總成本最低。
①代數式:不等式Y=a+b≥24ab。其中a和b均大於或等於0,當且僅當a=b時,Y有最小值2 4ab。所以現金持有相關總成本函數TC=TO+TS(其中TO表示機會成本,TS表示短缺成本,TO和TS均大於或等於0)應該在TO=TS時取最小值。
②微分法:現金持有相關總成本函數TC=TO+TS(其中TO表示機會成本對現金持有量的函數,TS表示短缺成本對現金持有量的函數,TO和TS均大於或等於O)如有極值,必然在其一階導數為零時。亦即 ,
, ,此時,TO成本曲線和TS成本曲線相交,TO=TS,TC有最小值。
,此時,TO成本曲線和TS成本曲線相交,TO=TS,TC有最小值。
綜上分析,我們可以得出,在採用成本分析模式確定最佳現金持有量時,由於只考慮與現金持有量有關的機會成本和短缺成本(其中機會成本與現金持有量呈正相關,短缺成本與現金持有量呈負相關)構成的總成本,總成本最低時的現金持有量為最佳現金持有量,此時,現金的機會成本等於其短缺成本。
運用成本分析模式確定最佳現金持有量的具體步驟不變,在採用數據進行過程分析時,應依數理及成本分析模式本身的內在規定,重新進行數據設計,以使其更加合理。根據相關成本與現金持有量之間的依存關係,相關測算數據設計如下:某企業現有ABCD四種現金持有方案,有關成本資料如下表。
現金持有量備選方案表
| 項目 | A | B | C | D |
| 現金持有量 | 100,000 | 200,000 | 300,000 | 400,000 |
| 機會成本率 | 10% | 10% | l0% | l0% |
| 短缺成本 | 48,000 | 25,000 | l0,000 | 5,000 |
根據上表採用成本分析模式編製該企業最佳現金持有量測算表數據如下表:
企業最佳現金持有量數據測算表
| 方案及現金持有量 | 機會成本 | 短缺成本 | 相關總成本 |
| A(100000) | 10,000 | 48,000 | 58,000 |
| B(200000) | 20,000 | 18,000 | 38,000 |
| C(300000) | 30,000 | 10,000 | 40,000 |
| D(400000) | 40,000 | 5,000 | 45,000 |
通過比較分析上表中各方案的總成本,由於B方案的相關總成本最低(38,000元),因此,企業選擇持有200,000元現金,即最佳現金持有量為200,000元。
在實際工作中,由於現金持有量、機會成本和短缺成本取值呈非連續性,所以採用逐步逼近的測試方法必然能夠找到較適宜的現金持有量。其基本思路就是沿著機會成本和短缺成本趨於相等的方向去尋找。
- ↑ 竹懷巨集.運用成本分析模式確定最佳現金持有量[J].中國西部科技,2006,(23)








B方案的短缺成本不是25000嗎?怎麼成了18000呢?