巴拿赫不動點定理
出自 MBA智库百科(https://wiki.mbalib.com/)
巴拿赫不動點定理(Banach fixed-point theorem)
目錄 |
巴拿赫不動點定理是指度量空間理論的一個重要工具。它保證了度量空間的一定自映射的不動點的存在性和唯一性,並提供了求出這些不動點的構造性方法。這個定理是以斯特凡•巴拿赫命名的,他在1922年提出了這個定理。
設(X, d)為非空的完備度量空間。設T : X → X為X上的一個壓縮映射,也就是說,存在一個非負的實數q < 1,使得對於所有X內的x和y,都有:
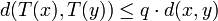
那麼映射T在X內有且只有一個不動點x * (這就是說,Tx * = x * )。更進一步,這個不動點可以用以下的方法來求出:從X內的任意一個元素x0開始,並定義一個迭代序列xn = Txn − 1,對於n = 1,2,3,……。這個序列收斂,且極限為x * 。以下的不等式描述了收斂的速率:
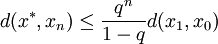
等價地:
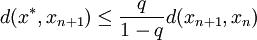
且
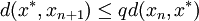
滿足以上不等式的最小的q有時稱為利普希茨常數。
註意對於所有不同的x和y都有d(Tx, Ty) < d(x, y)的要求,一般來說是不足以保證不動點的存在的,例如映像T : [1,∞) → [1,∞),T(x) = x + 1/x,就沒有不動點。但是,如果空間X是緊空間,則這個較弱的假設也能保證不動點的存在。
當實際應用這個定理時,最艱難的部分通常是恰當地定義X,使得T實際上把元素從X映像到X,也就是說,Tx總是X的一個元素。
選擇任何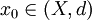 。對於每一個
。對於每一個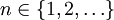 ,定義
,定義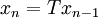 。我們聲稱對於所有的
。我們聲稱對於所有的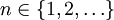 ,以下等式都成立:
,以下等式都成立:
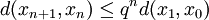 。
。
我們用數學歸納法來證明。對於n = 1的情況,命題是成立的,這是因為:
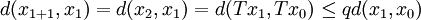 。
。
假設命題對於某個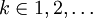 是成立的。那麼,我們有:
是成立的。那麼,我們有:

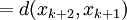
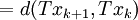
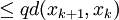
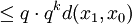
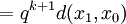 。
。
從第三行到第四行,我們用到了歸納假設。根據數學歸納法原理,對於所有的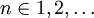 ,以上的命題都成立。
,以上的命題都成立。
設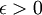 。由於
。由於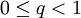 ,我們便可以找出一個較大的
,我們便可以找出一個較大的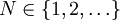 ,使得:
,使得:
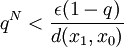 。
。
利用以上的命題,我們便有對於任何m,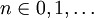 以及
以及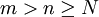 ,都有:
,都有:
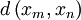
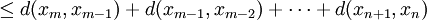
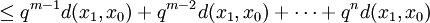
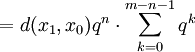
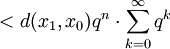
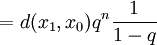

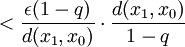
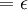 。
。
第一行的不等式可以從三角不等式推出;第四行的級數是一個幾何級數,其中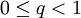 ,因此它收斂。以上表明
,因此它收斂。以上表明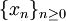 是
是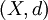 內的一個柯西序列,所以根據完備性,它是收斂的。因此設
內的一個柯西序列,所以根據完備性,它是收斂的。因此設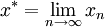 。我們作出兩個聲明:第一,
。我們作出兩個聲明:第一,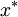 是
是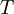 的一個不動點,也就是說,
的一個不動點,也就是說,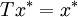 ;第二,
;第二,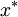 是
是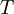 在
在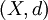 中的唯一的不動點。
中的唯一的不動點。
為了證明第一個命題,我們註意到對於任何的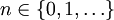 ,都有:
,都有:
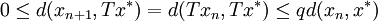 。
。
由於當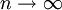 時,
時,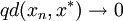 ,因此根據夾擠定理,可知
,因此根據夾擠定理,可知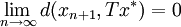 。這表明當
。這表明當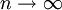 時,
時,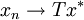 。但當
。但當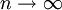 時,
時,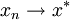 ,且極限是唯一的;因此,一定是
,且極限是唯一的;因此,一定是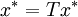 的情況。
的情況。
為了證明第二個命題,我們假設 也滿足
也滿足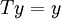 。那麼:
。那麼:
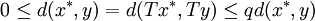 。
。
由於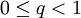 ,因此上式意味著
,因此上式意味著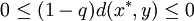 ,這表明
,這表明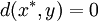 ,於是根據正定性,
,於是根據正定性,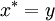 ,定理得證。
,定理得證。
巴拿赫不動點定理有許多逆定理,以下的一個是Czesław Bessaga在1959年發現的:
設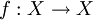 為一個抽象集合的映像,使得每一個迭代函數f^ n都有一個唯一的不動點。設q為一個實數,0 < q < 1。那麼存在X上的一個完備度量,使得f是壓縮映射,且q是壓縮常數。
為一個抽象集合的映像,使得每一個迭代函數f^ n都有一個唯一的不動點。設q為一個實數,0 < q < 1。那麼存在X上的一個完備度量,使得f是壓縮映射,且q是壓縮常數。







