數學歸納法
出自 MBA智库百科(https://wiki.mbalib.com/)
數學歸納法(mathematical induction,簡稱:MI)
目錄 |
數學歸納法(簡稱:MI)是一種數學證明方法,通常被用於證明某個給定命題在整個(或者局部)自然數範圍內成立。除了自然數以外,廣義上的數學歸納法也可以用於證明一般良基關係結構,例如:集合論中的樹(集合論)。這種廣義的數學歸納法應用於數學邏輯和電腦科學領域,稱作結構歸納法。
需要留意的是,數學歸納法雖然名字中有“歸納”,但是實際上數學歸納法並不屬於不嚴謹性(數學)的歸納法,實際上是屬於完全嚴謹的演繹推理法。
最簡單和常見的數學歸納法是證明當n等於任意一個自然數時某命題成立。證明分下麵兩步:
- 證明當n=0時命題成立。
- 證明如果在n=m時命題成立,那麼可以推導出在n=m+1時命題也成立。(m代表任意自然數)
這種方法的原理在於:首先證明在某個起點值時命題成立,然後證明從一個值到下一個值的過程有效。當這兩點都已經證明,那麼任意值都可以通過反覆使用這個方法推導出來。把這個方法想成多米諾效應也許更容易理解一些。例如:你有一列很長的直立著的多米諾骨牌,如果你可以:
- 證明第一張骨牌會倒。
- 證明只要任意一張骨牌倒了,那麼與其相鄰的下一張骨牌也會倒。
那麼便可以下結論:所有的骨牌都會倒。
用數學歸納法證題要恰當運用分析法,主要有如下三個步驟:
①歸納基礎:證n取第一個值時命題成立。
②證傳遞性:由成立證明時命題成立。
③得出結論:綜合,時命題成立。
假設我們要證明下麵這個公式(命題):
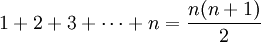
其中n為任意自然數。這是用於計算前n個自然數的和的簡單公式。證明這個公式成立的步驟如下。
第一步
第一步是驗證這個公式在n=0時成立。我們有左邊=0,而右邊=0(0+1)/2=0,所以這個公式在n=0時成立。第一步完成。
第二步
第二步我們需要證明如果假設n=m時公式成立,那麼可以推導出n=m+1時公式也成立。證明步驟如下。
我們先假設n=m時公式成立。即
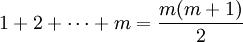 (等式1)
(等式1)
然後在等式等號兩邊分別加上m+1得到
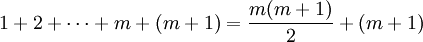 (等式2)
(等式2)
這就是n=m+1時的等式。我們現在需要根據等式1證明等式2成立。通過因式分解合併,等式2的右手邊
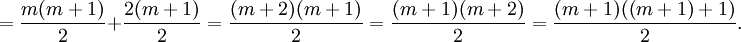
也就是說
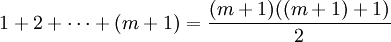
這樣便證明瞭從P(m)成立可以推導出P(m+1)也成立。證明至此結束,結論:對於任意自然數n,P(n)均成立。
在這個證明中,歸納推理的過程如下:
- 首先證明P(0)成立,即公式在n=0時成立。
- 然後證明從P(m)成立可以推導出P(m+1)也成立。(這裡實際應用的是演繹推理法)
- 根據上兩條從P(0)成立可以推導出P(0+1),也就是P(1)成立。
- 繼續推導,可以知道P(2)、P(3)也成立。
- 從P(3)成立可以推導出P(4)也成立。
- 不斷重覆推導下一命題成立的步驟。(這就是所謂“歸納”推理的地方)
- 我們便可以下結論:對於任意自然數n,P(n)成立。
在應用,數學歸納法常常需要採取一些變化來適應實際的需求。下麵介紹一些常見的數學歸納法變體。
如果我們想證明的命題並不是針對全部自然數,而只是針對所有大於等於某個數字b的自然數,那麼證明的步驟需要做如下修改:
- 第一步,證明當n=b時命題成立。
- 第二步,證明如果n=m(m≥b)成立,那麼可以推導出n=m+1也成立。
用這個方法可以證明諸如“當n≥3時,n2>2n”這一類命題。
如果我們想證明的命題並不是針對全部自然數,而只是針對所有奇數或偶數,那麼證明的步驟需要做如下修改:
奇數方面:
- 第一步,證明當n=1時命題成立。
- 第二步,證明如果n=m成立,那麼可以推導出n=m+2也成立。
偶數方面:
- 第一步,證明當n=0或2時命題成立。
- 第二步,證明如果n=m成立,那麼可以推導出n=m+2也成立。
數學歸納法並不是只能應用於形如“對任意的n”這樣的命題。對於形如“對任意的n=0,1,2,...,m”這樣的命題,如果對一般的n比較複雜,而n=m比較容易驗證,並且我們可以實現從k到k-1的遞推,k=1,...,m的話,我們就能應用歸納法得到對於任意的n=0,1,2,...,m,原命題均成立。
數學歸納法的原理作為自然數公理,通常是被規定了的(參見皮亞諾公理).但是他可以用一些邏輯方法證明;比如,如果下麵的公理:
- 自然數集是良序的。
註意到有些其他的公理確實的是數學歸納法原理中的二者擇一的公式化.更確切地說,兩個都是等價的.








666