超限歸納法

出自 MBA智库百科(https://wiki.mbalib.com/)

　　超限歸納法是數學歸納法的形式之一，可以應用於(大的)良序集，比如說應用到序數或基數，甚至於所有有序的集。是向(大)良序集合比如基數或序數的集合的擴展。

　　超限歸納法可用於證明一個函數P在所有序數中成立：

　　基礎：證明 P(0) 成立；

　　歸納：證明對於任何一個序數 b，如果 P(a) 在所有序數 a<b 中成立，那麼 P(b) 也將成立。

　　後面一步常常分解為兩種情況:

　　能應用和一般的歸納法相似的方法後繼序數 (有直接前驅的序數)，(P(a)蘊涵P(a+1))，

　　沒有前驅的極限序數，因此不能用這種方法。

　　顯然，極限序數可以通過極限序數b 是所有序數的上確界來處理；因為對於所有序數都有 a<b，所以假定在所有的 a<b 中 P(a) 成立，則證明瞭 P(b)。

　　上面的基礎步驟實際上是多餘的。如果在所有的 a<b 中，P(b) 獲得自 P(a) 為真，那麼 P(0) 成立就是一個簡單的特殊情況，因為在所有 a<0 中 P(a) 成立。

　　假設只要對於所有的β<α，P(β)為真，則P(α)也為真。那麼超限歸納告訴我們P對於所有序數為真。

　　就是說，如果P(α)為真只要P(β)對於所有β<α為真，則P(α)對於所有α為真。或者更實用的說:為了證明對於所有序數α的一個性質P，你可以假定它已經對於所有更小β<α是已知的。

　　通常證明被分為三種情況:

• 零情況:證明P(0)為真。

• 後繼情況:證明對於任何後繼序數β1，P(β1)得出自P(β) (如果必需的話，證明P(α)對於所有α<β)。

*極限情況:證明對於任何極限序數λ, P(λ)得出自[P(α)對於所有α<λ]。

　　註意第二和第三種情況是同一的，除了對於所考慮的序數類型不同之外。它們不是必須在形式上分開證明，但在實踐中它們的證明典型的非常不同而需要分別表述。

　　超限遞歸是密切相關於超限歸納概念的構造或定義某種東西的方法。例如，集合序列A_a被定義於所有的序數α，通過指定三個事情:

• A₀是什麼

• 如何確定A_a1自A_a (也可能從整個序列達到A_a)

• 對於極限序數λ，如何確定Aλ從A_a的對於α<λ的序列。

　　更形式的說，陳述超限遞歸定理如下。給定函數類G₁,G₂,G₃，存在一個唯一的超限序列F帶有dom(F)=Ord(Ord是所有序數的真類)使得

• F(α+1) = G₂(F(a))，對於所有

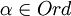
• F(α) =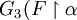)，對於所有極限

　　註意我們要求G₁,G₂,G₃的定義域足夠廣闊來使上述性質有意義。所以滿足這些性質的序列的唯一性可以使用超限歸納證明。

　　更一般的說，你可以在任何良序關係R上通過超限遞歸定義東西。 (R甚至不需要是集合；它可以是真類，假定它是類似集合的關係；就是說，對於任何x，使得yRx的所有y的搜集必定是集合。)

　　有一個常見的誤解是超限歸納或超限遞歸或二者要求選擇公理。這是錯誤的，超限歸納可以應用於任何良序集合。但是常見的情況是使用超限歸納的這種證明或構造也使用選擇公理來良序排序一個集合。

• 數學歸納法
• 結構歸納法
• epsilon-歸納