外部收益率
出自 MBA智库百科(https://wiki.mbalib.com/)
外部收益率(Extemal Rate of Retum,ERR)
目錄 |
外部收益率(ERR)是使一個投資方案原投資額的終值與各年的凈現金流量按基準收益率或設定的折現率計算的終值之和相等時的收益率。
外部收益率既是按統一的收益率計算各年的凈現金流量形成的增值,又可避免非常規方案的多個內部收益率問題,可彌補上述內部收益率指標的不足。
外部收益率的計算公式為:
-
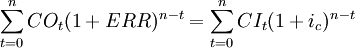 (1)
(1)
外部收益率可以說是對內部收益率的一種修正,計算外部收益率與內部收益率一樣假定建設項目在計算期內所獲得的凈收益全部用於再投資, 但不同的是假定再投資的收益率等於基準收益率。其經濟含義是:建設項目在基準收益率的利率下,在建設項目壽命終了時, 以每年的凈收益率恰好把投資全部收回。
外部收益率法用於建設項目經濟效果評價時,也需要與基準收益率ic 比較,其獨立建設項目評判準則為:外部收益率( ERR )大於等於基準收益率ic時,建設項日可行;否則,建設項目不可行。
外部收益率法用於多個可行建設項目的優選與排序時,其評判準則為:外部收益率越大的建設項目越優。
內部收益率(IRR)與外部收益率(ERR)均考慮了建設項目計算期內的資金時間價值,它們既有共性又有區別,深入分析它們之間的關係, 對於在建設項目經濟評價中能否運用外部收益率替代內部收益率具有重要的意義。
(一)當IRR > ic 時。
將式(1)的等號兩邊同時乘以(1 + IRR)n ,得:
-
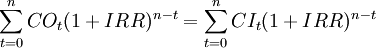 (2)
(2)
- ∵IRR > ic
- ∴
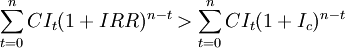 (3)
(3)
由式(1) 、式(2)及式(3)得:
-
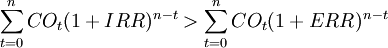 (4)
(4)
- ∴IRR > ERR
- 又∵IRR >ic
∴建設項目可行
所以當用ic 來計算建設項目的終值時,現金流出量的終值應小於現金流入量的終值,即用ic 替換式(2)中的IRR,得:
-
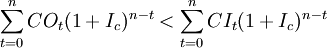 (5)
(5)
由式(1)及式(5)得:
- ∴ERR > ic故IRR > ERR > ic
即當IRR > ic 時, IRR > ERR > ic。
(二)當IRR < ic 時當式(1)的等號兩邊同乘以(1 + IRR)n ,得:
-
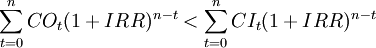 (6)
(6)
- ∵IRR < ic
- ∴
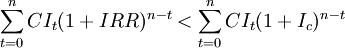 (7)
(7)
由式(1) 、式(6)及式(7)得:
-
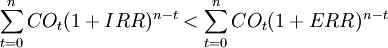 (8)
(8)
- ∴IRR < ERR
- 又∵IRR < ic
∴建設項目是不可行
所以當用ic 來計算建設項目的終值時,現金流出量的終值應大於現金流入量的終值,即用ic 替換式(6)中的IRR,得:
-
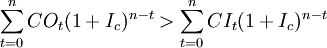 (9)
(9)
由式(1)及式(9)得:
- ∴ERR < ic。
故IRR < ERR < ic。
即當IRR < ic 時, IRR < ERR < ic
綜上所述,內部收益率和外部收益率的關係為:
當IRR > ic 時, IRR > ERR > ic;當IRR < ic 時, IRR <ERR < ic。因此,內部收益率法和外部收益率法評判的結果是一致的。
常規建設項目的外部收益率往往不能準確地反映其建設項目投入資金年動態收益率的大小 , 而且對於多次投資且壽命周期比較長的建設項目來說,外部收益率的計算也比較麻煩, 需要求解諸如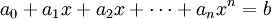 ( n ≥3)的高次一元方程。但相對於內部收益率法來說, 外部收益率法具有內部收益率法無法比擬的優點:
( n ≥3)的高次一元方程。但相對於內部收益率法來說, 外部收益率法具有內部收益率法無法比擬的優點:
(1)對於非常規建設項目, 由外部收益率的計算公式可知,其方程不會出現多個正實數解的情況,只有唯一解,這就避免了非常規建設項目存在多個內部收益率的問題,這是外部收益率的一大優點。
(2)外部收益率法中各年現金流出量按外部收益率折現後的終值, 等於各年現金流入量按基準收益率再投資後得到的終值。這樣就剋服了建設項目尚未回收的投資和建設項目回收取得的資金都能獲得相同的收益率的弊病。
(3)外部收益率法所用的再投資報酬率是基準收益率,而基準收益率是根據特定的經濟環境、資金市場、投資項目以及特定的時期用科學方法進行預測得到的,是使建設項目可行的最低要求,因此外部收益率與實際再投資報酬率更為接近。
(4)由於外部收益率表示建設項目在計算期內按基準收益率將獲得的凈收益全部用於再投資的收益水平,因而,對於多個可行建設項目的比選,就不必運用內部收益率類似的方法—兩差額比較,則可直接採取各建設項目外部收益率的值直接進行優劣排序,從而大大簡化了比選過程。
因此,外部收益率不僅比內部的收益率計算簡便,而且其計算結果更為客觀正確,在投資決策中更能為決策者提供可靠有用的信息。
設某投資方案的現金流動表如下表-1所示:
表-1
年 度 凈現金流量 0 -20 000 1-5 5 600 5 4 000
其外部收益率按下列方法計算(設要求達到的最低收益率為10%):
按要求達到的最低收益率計算各年凈現金流入量到壽命期終了時的終值之和:
5 600×(F/A,10%,5)+4 000=38 188(元)
上述終值之和相當於原投資額至方案壽命期終了時的本利和,可據以推算原 投資額在方案壽命期內取得的收益率:
終值繫數:(F/P,ERR,5)=38 188÷20 000=1.9094
從複利終值表中找出在相同期數里與上述繫數相鄰的折現率,再依據兩個相鄰的折現率和已計算的終值繫數,用“內插法”計算出方案的收益率為13.807%。
評論(共2條)
n 0.5% 1% 1.5% 2% 2.5% 3% 3.5% 4% 5% 6% 7% 8% 1 1.005 1.01 1.015 1.02 1.025 1.03 1.035 1.04 1.05 1.06 1.07 1.08 2 1.010 1.020 1.030 1.040 1.050 1.060 1.071 1.081 1.102 1.123 1.144 1.166 3 1.015 1.030 1.045 1.061 1.076 1.092 1.108 1.124 1.157 1.191 1.225 1.259 4 1.020 1.040 1.061 1.082 1.103 1.125 1.147 1.169 1.215 1.262 1.310 1.360 5 1.025 1.051 1.077 1.104 1.131 1.159 1.187 1.216 1.276 1.338 1.402 1.469 6 1.030 1.061 1.093 1.126 1.159 1.194 1.229 1.265 1.340 1.418 1.500 1.586
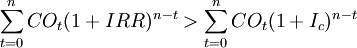
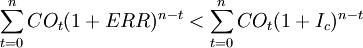








從複利終值表中找出在相同期數里與上述繫數相鄰的折現率? 在繫數表中就找不到n=5,對應的折現率能包含這兩個的呢?