馬科維茨的均值一方差組合模型
出自 MBA智库百科(https://wiki.mbalib.com/)
馬科維茨的均值一方差組合模型(Markowitz Mean-Variance Model,Markowitz Model簡稱MM)
目錄[隱藏] |
證券及其它風險資產的投資首先需要解決的是兩個核心問題:即預期收益與風險。 那麼如何測定組合投資的風險與收益和如何平衡這兩項指標進行資產分配是市場投資者迫切需要解決的問題。正是在這樣的背景下,在50年代和60年代初,馬可維茲理論應運而生。
該理論依據以下幾個假設:
1、投資者在考慮每一次投資選擇時,其依據是某一持倉時間內的證券收益的概率分佈。
2、投資者是根據證券的期望收益率估測證券組合的風險。
3、投資者的決定僅僅是依據證券的風險和收益。
4、在一定的風險水平上,投資者期望收益最大;相對應的是在一定的收益水平上,投資者希望風險最小。
根據以上假設,馬可維茲確立了證券組合預期收益、風險的計算方法和有效邊界理論,建立了資產優化配置的均值-方差模型:
目標函數:minб2(rp)=∑ ∑xixjCov(ri,rj)
rp= ∑ xiri
限制條件: 1=∑Xi (允許賣空)
或 1=∑Xi xi>≥0(不允許賣空)
其中rp為組合收益, ri為第i只股票的收益,xi、 xj為證券 i、j的投資比例,б2(rp)為組合投資方差(組合總風險),Cov (ri 、rj ) 為兩個證券之間的協方差。該模型為現代證券投資理論奠定了基礎。上式表明,在限制條件下求解Xi 證券收益率使組合風險б2(rp )最小,可通過朗格朗日目標函數求得。其經濟學意義是,投資者可預先確定一個期望收益,通過上式可確定投資者在每個投資項目(如股票)上的投資比例(項目資金分配),使其總投資風險最小。不同的期望收益就有不同的最小方差組合,這就構成了最小方差集合。
馬科維茨的投資組合理論不僅揭示了組合資產風險的決定因素,而且更為重要的是還揭示了“資產的期望收益由其自身的風險的大小來決定”這一重要結論,即資產價格(單個資產和組合資產)由其風險大小來定價,單個資產價格由其方差或標準差來決定,組合資產價格由其協方差來決定。馬可維茨的風險定價思想在他創建的“均值-方差”或“均值-標準差”二維空間中投資機會集的有效邊界上表現得最清楚。下文在“均值-標準差”二維空間中給出投資機會集的有效邊界,圖形如下:
上面的有效邊界圖形揭示出:單個資產或組合資產的期望收益率由風險測度指標標準差來決定;風險越大收益率越高,風險越小收益率越低;風險對收益的決定是非線性(二次)的雙曲線(或拋物線)形式,這一結論是基於投資者為風險規避型這一假定而得出的。具體的風險定價模型為:
其中![]() ,且A,B,C,D為常量;R表示N個證券收益率的均值(期望)列向量,Ω為資產組合協方差矩陣,1表示分量為1的N維列向量,上標T表示向量(矩陣)轉置(公式(5)的推導過程。
,且A,B,C,D為常量;R表示N個證券收益率的均值(期望)列向量,Ω為資產組合協方差矩陣,1表示分量為1的N維列向量,上標T表示向量(矩陣)轉置(公式(5)的推導過程。
馬可維茨的風險定價思想和模型具有開創意義,奠定了現代金融學、投資學乃至財務管理學的理論基礎。不過這種理論也有缺點,就是他的數學模型較為複雜,不便於實際操作。

 无广告阅读
无广告阅读  免验证复制
免验证复制  微信支付
微信支付  支付宝
支付宝  PayPal
PayPal 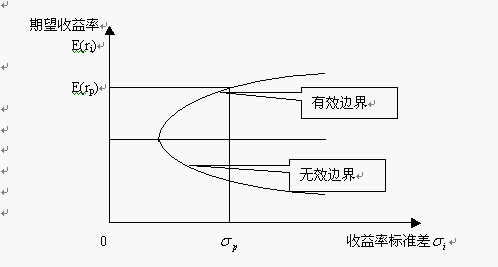











本欄目辦得好