單峰偏好理論
出自 MBA智库百科(https://wiki.mbalib.com/)
單峰偏好理論(Single Peak Preference Theory)
目錄 |
單峰偏好理論是由鄧肯·布萊克(Duncan Black)在1958年出版的《委員會與選舉理論》一書中做出的。擬通過修正阿羅五原則解決投票悖論。其內容是限定每個選民的偏好只能有一個峰值。
所謂單峰偏好,是指選民在一組按某種標準排列的備選方案中,有一個最為偏好的選擇,而從這個方案向任何方面的偏離,選民的偏好程度或效用都是遞減的。如果一個人具有雙峰或多峰偏好,則他從最為偏好的方案偏離時,其偏好程度或效用會下降,但之後會再上升。布萊克證明瞭如果假設各個選民的偏好都是單峰偏好,那麼最終投票的結果就可以避免阿羅悖論,社會成員個人的偏好之和可以得出確定的唯一的社會總體偏好,而這種社會總體偏好恰好是個人偏好處於所有選民偏好峰的中點上的選民,高於他偏好的選民數量和低於他偏好的選民數量正好相等,這也就是著名的中間投票人模式(median voter models)。布萊克由於對這個問題的開創性研究而被戈登·塔洛克(Gordon Tullock)稱為公共選擇學派的奠基人。
鄧肯·布萊克認為,通過對個人的偏好進行適當限制,使其適合於某一種類型,則多數決策結果就滿足可傳遞性假定。布萊克對個人偏好提出的特殊類型就是具有單峰形狀。這種單峰形狀的個人偏好類型可被說明如下 (表1):
- 表1 單峰形狀的個人偏好
| 第一選擇 | 第二選擇 | 第三選擇 | |
|---|---|---|---|
| 個人1 | A | B | C |
| 個人2 | C | B | A |
| 個人3 | B | C | A |
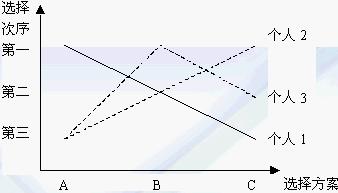
我們可以對A、B、C三種選擇目標進行比較:當A與B相比較時,B將勝於A;當B與C比較時,B仍將勝於C;當A與C比較時,C將勝於A。這樣,在以上例子中,給定一個特殊的個人偏好結構,多數決策的結果滿足可傳遞性,社會選擇的偏好順序將是BpCpAp(這裡p表示“偏好(prefer)”,即前者比後者更可取)。為什麼稱上表所示的個人偏好類型為單峰型呢?可以用下圖加以說明。
(圖1)
假定有三個人l、2、3,每人共同面臨A、B、C三種選擇,A代表政府高水平的預算,B代表中等水平的預算,C代表低水平的預算。每個人的偏好順序以他對於這三個選擇方案的排列順序表示出來。表4-1代表這三個人的偏好順序:
- 表2 個人的偏好順序
| 第一選擇 | 第二選擇 | 第三選擇 | |
|---|---|---|---|
| 個人1 | A | B | C |
| 個人2 | B | C | A |
| 個人3 | C | A | B |
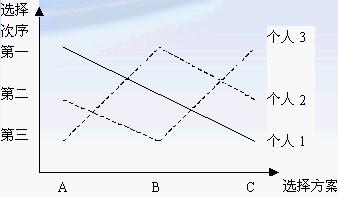
(圖2)
圖2表示表2上的個人偏好結構,而圖1表示表1上的個人偏好結構。圖2與圖1的區別在於,在圖4-2中,三個人的偏好線都是單峰形狀的。單峰偏好意味著人們最理想的結果只有一個,對於這個惟一的最理想目標的偏離,無論是正的方向,還是負的方向,都是壞事情,都將使他們的福利水平降低。例如,對於個人1來講,如果選擇方案依照A、B、C的順序排列,他會認為境況逐漸變壞;對於個人2來講,如果選擇方案依照A、B、C的順序排列,他會認為境況逐漸變好;對於個人3來講,只要偏離了B方案,不論是向哪個方向偏離,他都認為境況變壞。而在圖4-1中,個人3的偏好線是雙峰形的(多峰偏好),該線先是從某一峰頂上往下降,然後又往另一峰頂上升。多峰偏好則意味著人們最理想的結果不止一個。最初,當人們偏離其最偏好的選擇目標時,境況會因此變壞,若繼續沿著這個方向運動,其境況則會最終變好。
在現實中,多峰偏好可能是在許多問題上所出現的共同現象。比如,一位對公立學校預算計划進行投票表決的投票人就有可能具有多峰偏好。假定投票人既可以將孩子送到私立學校就學,也可以送到公立學校就學,並假定決定投票人在送孩子到哪種學校就學態度上的因素,在於公立學校的質量,而公立學校的質量又與其預算規模正相關。
該投票人的第一選擇可能是將他的孩子送到私立學校。如果他這樣做,儘量壓縮公立學校的預算開支就會符合他的利益,這是因為他雖然為公立學校繳納稅款,但是並沒有從中獲得直接利益。因此,他的第一選擇就是制定符合最低質量公立學校的預算計劃。如果假定學校預算所需要的稅收足以允許建立一所中等質量的公立學校,投票人繳納稅收之後的收入在支付孩子私立學校就學費用上發生困難,或者認為送孩子到私立學校就學不再划算,他就會轉而支持一個可以維持高質量的公立學校的預算,把孩子送到公立學校就學。所以,他的第二選擇是一個儘可能提高公立學校教學質量的預算方案,而維持中等質量的公立學校的預算,對他來講,是一種最差的選擇。
一些國家的公民在對待戰爭問題上,有時也會出現多峰偏好的傾向。例如在越南戰爭時期,許多美國公眾更傾向於完全投入戰爭(包括使用核武器)或完全不參與戰爭,而對進行一場有限戰爭和局部戰爭不太感興趣。可以看出,這些公民對於極端性解決方案,而不是折中性解決方案表示出更大的偏好。也正是由於多峰偏好的存在才使得在多數票規則下有可能無法達成政治均衡。
對比多峰偏好,對於單峰型的個人偏好結構可以有以下結論:
1、在單峰型的個人偏好結構中,多數決策的結果具有穩定性。在2的表式中,社會偏好不具有傳遞性,是迴圈的,於是,投票結果是不確定的。現在,在單峰偏好下,迴圈被打破了,從而產生了一個穩定的結果。
2、單峰偏好雖然剋服了投票悖論,但它違反了阿羅關於“無限制的定義域”的假定,即單峰偏好是依靠把個人偏好限制在單峰狀態為前提的。
3、單峰狀態究竟在實際中是否存在?布萊克認為,在大多數場合,個人的偏好結構會呈現出單峰形。為什麼呢?由於A代表低水平的預算,B代表中等水平的預算,C代表高水平的預算,在概率上說,CpApBp的個人偏好順序出現的可能性很小,因為絕大多數人不會既認為高額預算比低額預算好,又認為低額預算比中等規模的預算好。
1970年,圖洛克與坎貝爾(Campbell)在《小型投票體系的電腦模擬》(Computer simulation of a small voting system)一文中指出,在現實世界中,投票者的人數總是大大超過供投票選擇的社會狀態的個數的。這時,出現投票悖論的概率是如此的小,以至於在實際中可以不考慮它。這時,出現一致的概率就很高,而再提出或擁護另一個選擇方案的成本會高於該方案能帶來的利益。如果實際的多數投票結果確實靠近中間狀態,則該結果將被大家所接受。雖然,圖洛克的分析是否有效,這個問題是有待於經驗證明的,但是,可以肯定的是,圖洛克這一段話是非常有助於說明直接民主投票制與間接投票制之間的差異的。
1、在直接民主投票制下,參加投票的人數總是大大超過被投票表決的方案個數的,這時出現投票悖論概率很小。
2、在代表制投票方式(間接投票制)下,如在英國,投票者總是限於保守黨、工黨與別的大黨之間,由於投票者數目減少了,就使投票難以達到一致的結果。
這說明,在一個社會可供選擇的狀態的個數已定的前提下,決策程式越是不民主,則投票結果就越是不確定、不穩定,政府政策就越是易變,於是,也會越是依賴於專制型決策。








哪來的阿羅五原則?不是四原則?