加權算術平均指數
出自 MBA智库百科(https://wiki.mbalib.com/)
目錄 |
加權算術平均指數是以基期總量為權數對個體數量指標指數進行加權算術平均,以此計算的加權平均數指數等於數量指標綜合指數。
加權算術平均指數=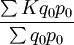
上式中,K表示數量指標的個體指數,表示基期的某個總量指標。也就是說,要編製加權算術平均數指數,一要掌握數量指標個體指數,二要掌握基期總量。
當已知數量指標的個體指數Kq,或報告期與基期的個體數量指標ql、q0,以及基期的總量指標(產值或銷售額)p0q0並以其作為權數時;同樣,已知質量指標的個體指數kp,或報告期與基期的個體價格指標p1、p0 及報告期的總量指標(產值或銷售額)p1q1為權數時,即可分別計算數量指標的總指數及質量指標的總指數 。即:
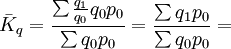 數量指標綜合指數
數量指標綜合指數
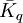 :為加權平均數量指標指數;
:為加權平均數量指標指數;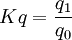 為數據指標的個體指數。
為數據指標的個體指數。
由上式可知,在一定條件下,加權算術平均指數是拉氏綜合指數的變形。同時只有用q0p0為權數的情況下加權,加權算術平均指數才可能與拉氏綜合指數相互轉換變為綜合指數。如果權數不是P0q0,而使用p0q0以外的任何其它權數進行加權,加權算術平均指數就不可能等於綜合指數,當然,這種變形關係也就不復存在。
在用拉氏綜合指數公式計算商品銷售量指數時,必須掌握基期和報告期各種商品的銷售量及基期各種商品的價格資料。但在實踐中,按基期價格與報告期銷售量所計算的假定銷售額(p0ql)資料不易取得,而基期的銷售額資料(p0q0)與各種商品的銷售量個體指數卻很容易取得。所以,加權算術平均指數適用於數量指標平均數指數的計算。








能不能舉個淺顯易懂的例子呢? 光看公式太晦澀難懂了