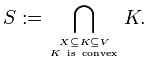凸包
出自 MBA智库百科(https://wiki.mbalib.com/)
凸包（Convex hull）
目錄 |
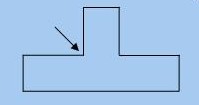
在瞭解凸包之前，須先認識何謂“凸多邊形”(Convex Polygon)。從直觀上說，一個凸多邊形就是沒有任何凹陷位的多邊形。我們在低年級數學所學習的三角形、正方形、長方形、平行四邊形、正五邊形、正六邊形等等，都是凸多邊形的例子。但是以下這個“凸”字形卻並非凸多邊形，因為箭頭指著的地方實際是一個凹陷位。
可是上述這一定義很不嚴密，究竟何謂“凹陷位”？實在難以說清楚。因此在數學上，凸多邊形有另一個嚴格的定義。假設我們在一個多邊形上(包括多邊形的邊界及邊界圍封的範圍)任意取兩點並以一條線段連結該兩點，如果線段上的每一點均在該多邊形上，那麼我們便說這個多邊形是凸的。根據以上定義，我們便可判斷“凸”字形的確不是凸的。例如，在下圖中，連結A、B兩點的線段有一部分並不在該多邊形上。
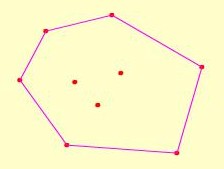
認識了凸多邊形後，我們便可瞭解何謂凸包。給定平面上的一個(有限)點集(即一組點)，這個點集的凸包就是包含點集中所有點的最小面積的凸多邊形。例如，下圖的點集共包含9個點，圖中的六邊形便是該點集的凸包。其中構成六邊形的6個點稱為“凸包上的點”(Hull Point)，其餘3個點則並非“凸包上的點”。請註意上述定義中“最小面積”這個限制條件，因為除了凸包以外，還有無限多個包含點集中所有點的凸多邊形。例如，只要畫一個面積足夠大的四邊形，便可包圍任意給定的點集。因此假如沒有這個限制條件，求凸包就變成非常容易但卻沒有唯一解的運算。
在一個實數向量空間V中，對於給定集合X，所有包含X的凸集的交集S被稱為X的凸包。
X的凸包可以用X內所有點(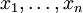
)的線性組合來構造。
![S:=\begin{Bmatrix} \sum_{j=1}^nt_jx_j|x_j\in X,\sum_{j=1}^nt_j=1,t_j\in[0,1] \end{Bmatrix}](/w/images/math/d/9/b/d9b608cdd3c4ab201af1a906d5ac7fb2.png)
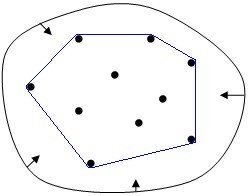
在二維歐幾裡得空間中，凸包可想象為一條剛好包著所有點的橡皮圈。
增量式演算法1
逐次再點加入，然後檢查之前的點是否在新的凸包上。由於每次都要檢查所有之前的點，時間複雜度為O(n2)。
包裹法(Jarvis步進法)
首先由一點必定在凸包的點開始，例如最左的一點A1。然後選擇A2點使得所有點都在A1A2的右方，這步驟的時間複雜度是O(n)，要比較所有點以A1為原點的極坐標角度。以A2為原點，重覆這個步驟，依次找到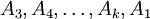
。這總共有k步。因此，時間複雜度為O(n2)。
葛立恆掃描法
由最底的一點A1開始，計算它跟其他各點的連線和x軸的角度，按小至大將這些角度排序，稱它們的對應點為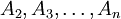
。這裡的時間複雜度可達O(nlogn)。
考慮最小的角度對應的點A3。若由A2到A3的路徑相對A1到A2的路徑是向右轉的（可以想象一個人沿A1走到A2，他站在A2時，是向哪邊改變方向），表示A3不可能是凸包上的一點，考慮下一點由A2到A4的路徑；否則就考慮A3到A4的路徑是否向右轉……直到回到A1。
這個演算法的整體時間複雜度是O(nlogn)，註意每點只會被考慮一次，而不像Jarvis步進法中會考慮多次。
這個演算法由葛立恆在1972年發明。[1]它的缺點是不能推廣到二維以上的情況。
單調鏈
將點按x坐標的值排列，再按y坐標的值排列。
選擇x坐標為最小值的點，在這些點中找出y坐標的值最大和y坐標的值最小的點。對於x坐標為最大值也是這樣處理。將兩組點中y坐標值較小的點連起。在這條線段下的點，找出它們之中y坐標值最大的點，又在它們之間找x坐標值再最小和最大的點……如此類推。
時間複雜度是O(n log n)。
分治法
將點集X分成兩個不相交子集。求得兩者的凸包後，計算這兩個凸包的凸包，該凸包就是X的凸包。時間複雜度是O(n log n)。
快包法(Akl-Toussaint啟髮式)
選擇最左、最右、最上、最下的點，它們必組成一個凸四邊形（或三角形）。這個四邊形內的點必定不在凸包上。然後將其餘的點按最接近的邊分成四部分，再進行快包法(QuickHull)。
- ↑ Graham,R.L.(1972).An Efficient Algorithm for Determining the Convex Hull of a Finite Planar Set.Information Processing Letters 1,132-133
