凱萊-哈密頓定理
出自 MBA智库百科(https://wiki.mbalib.com/)
目錄[隱藏] |
線上性代數中,凱萊-哈密頓定理(以數學家阿瑟•凱萊與威廉•盧雲•哈密頓命名)表明每個布於任何交換環上的實或復方陣都滿足其特征方程式。
明確地說:設 A 為給定的  矩陣,並設 In 為
矩陣,並設 In 為  單位矩陣,則 A 的特征多項式定義為:
單位矩陣,則 A 的特征多項式定義為:
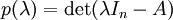
其中 det 表行列式函數。凱萊-哈密頓定理斷言:
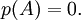
凱萊-哈密頓定理等價於方陣的特征多項式會被其極小多項式整除,這在尋找若爾當標準形時特別有用。
以下考慮布於域 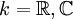 上的矩陣。
上的矩陣。
凱萊-哈密頓定理可以視為線性代數中克萊姆法則的推論。克萊姆法則斷言:若 S 是  矩陣,而 cof(S) 表其餘因數矩陣,則
矩陣,而 cof(S) 表其餘因數矩陣,則
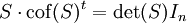
取 S: = tIn − A,便得到 (tIn − A)cof(tIn − A)t = pA(t)In。此式對所有 t 皆成立,由於實數或複數域有無窮多元素,上式等式在多項式環 k[t] 內成立。
設 M: = kn,矩陣 A 賦予 M 一個 k[t]-模結構: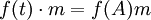 。考慮 k[t]-模
。考慮 k[t]-模 ![M[t] := M \otimes_k k[t]](/w/images/math/a/e/e/aee5ff35e91446923022b3807137ca79.png) ,我們有 k[t]-模之間的「求值態射」:
,我們有 k[t]-模之間的「求值態射」:
![e_A: M[t] \to M, \qquad M \otimes t^i \mapsto A^i m](/w/images/math/9/c/7/9c73897b8f0b5259287f95523839411e.png)
固定 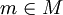 ,對 M[t] 中的等式
,對 M[t] 中的等式
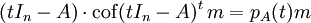
右側取 eA 後得到 pA(A)m,左側取 eA 後得到 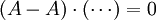 。明所欲證。
。明所欲證。
一個簡單的證明:
令:
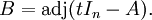
由:
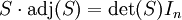
得:
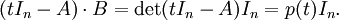
將上式左邊按t進行多項式展開得:
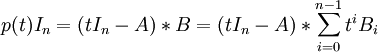
=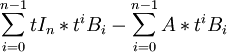
=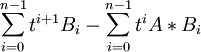
=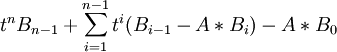
將上式右邊展開得:
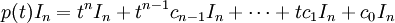
因兩多項式,他們的對應項繫數相等得:
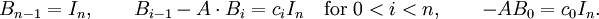
在等式兩邊t的i次項繫數分別乘以Ai, 並將等式左右兩邊分別相加併合項得:

得證。
前述證明用到繫數在 k[t] 的矩陣的克萊姆法則,事實上該法則可施於任何繫數在交換環上的矩陣。藉此,凱萊-哈密頓定理可以推廣到一個交換環 R 上的任何有限生成自由模 M(向量空間是特例)。中山正引理的一種證明就用到這個技巧。
舉例明之,考慮下述方陣:
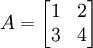
其特征多項式為
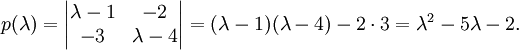
此時可以直接驗證凱萊-哈密頓定理:
A2 − 5A − 2I2 = 0
此式可以簡化高次冪的運算,關鍵在於下述關係:
A2 − 5A − 2I2 = 0
A2 = 5A + 2I2.
例如,為了計算 A4,可以反覆利用上述關係式:
A3 = (5A + 2I2)A = 5A2 + 2A = 5(5A + 2I2) + 2A = 27A + 10I2
A4 = A3A = (27A + 10I2)A = 27A2 + 10A = 27(5A + 2I2) + 10A
A4 = 145A + 54I2.
此外,凱萊-哈密頓定理也是計算特征向量的重要工具。
註:一般而言,若  矩陣 A 可逆(即:
矩陣 A 可逆(即: ),則 A − 1 可以寫成 A 的冪次和:特征多項式有如下形式
),則 A − 1 可以寫成 A 的冪次和:特征多項式有如下形式
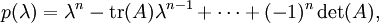
将方程式 p(A) = 0 同乘以 A − 1,便得到
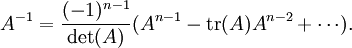

 无广告阅读
无广告阅读  免验证复制
免验证复制  微信支付
微信支付  支付宝
支付宝  PayPal
PayPal 













