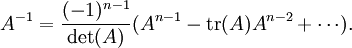凯莱-哈密顿定理
出自 MBA智库百科(https://wiki.mbalib.com/)
目录 |
在线性代数中,凯莱-哈密顿定理(以数学家阿瑟•凯莱与威廉•卢云•哈密顿命名)表明每个布于任何交换环上的实或复方阵都满足其特征方程式。
明确地说:设 A 为给定的  矩阵,并设 In 为
矩阵,并设 In 为  单位矩阵,则 A 的特征多项式定义为:
单位矩阵,则 A 的特征多项式定义为:
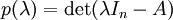
其中 det 表行列式函数。凯莱-哈密顿定理断言:
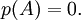
凯莱-哈密顿定理等价于方阵的特征多项式会被其极小多项式整除,这在寻找若尔当标准形时特别有用。
以下考虑布于域 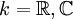 上的矩阵。
上的矩阵。
凯莱-哈密顿定理可以视为线性代数中克莱姆法则的推论。克莱姆法则断言:若 S 是  矩阵,而 cof(S) 表其余因子矩阵,则
矩阵,而 cof(S) 表其余因子矩阵,则
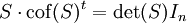
取 S: = tIn − A,便得到 (tIn − A)cof(tIn − A)t = pA(t)In。此式对所有 t 皆成立,由于实数或复数域有无穷多元素,上式等式在多项式环 k[t] 内成立。
设 M: = kn,矩阵 A 赋予 M 一个 k[t]-模结构: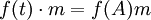 。考虑 k[t]-模
。考虑 k[t]-模 ![M[t] := M \otimes_k k[t]](/w/images/math/a/e/e/aee5ff35e91446923022b3807137ca79.png) ,我们有 k[t]-模之间的「求值态射」:
,我们有 k[t]-模之间的「求值态射」:
![e_A: M[t] \to M, \qquad M \otimes t^i \mapsto A^i m](/w/images/math/9/c/7/9c73897b8f0b5259287f95523839411e.png)
固定 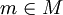 ,对 M[t] 中的等式
,对 M[t] 中的等式
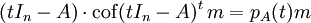
右侧取 eA 后得到 pA(A)m,左侧取 eA 后得到 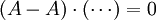 。明所欲证。
。明所欲证。
一个简单的证明:
令:
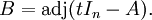
由:
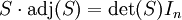
得:
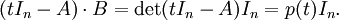
将上式左边按t进行多项式展开得:
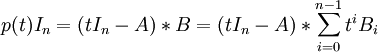
=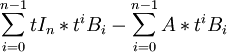
=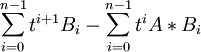
=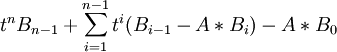
将上式右边展开得:
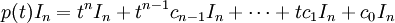
因两多项式,他们的对应项系数相等得:
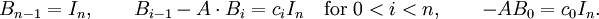
在等式两边t的i次项系数分别乘以Ai, 并将等式左右两边分别相加并合项得:

得证。
前述证明用到系数在 k[t] 的矩阵的克莱姆法则,事实上该法则可施于任何系数在交换环上的矩阵。藉此,凯莱-哈密顿定理可以推广到一个交换环 R 上的任何有限生成自由模 M(向量空间是特例)。中山正引理的一种证明就用到这个技巧。
举例明之,考虑下述方阵:
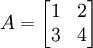
其特征多项式为
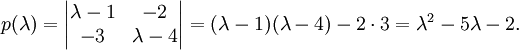
此时可以直接验证凯莱-哈密顿定理:
A2 − 5A − 2I2 = 0
此式可以简化高次幂的运算,关键在于下述关系:
A2 − 5A − 2I2 = 0
A2 = 5A + 2I2.
例如,为了计算 A4,可以反复利用上述关系式:
A3 = (5A + 2I2)A = 5A2 + 2A = 5(5A + 2I2) + 2A = 27A + 10I2
A4 = A3A = (27A + 10I2)A = 27A2 + 10A = 27(5A + 2I2) + 10A
A4 = 145A + 54I2.
此外,凯莱-哈密顿定理也是计算特征向量的重要工具。
注:一般而言,若  矩阵 A 可逆(即:
矩阵 A 可逆(即: ),则 A − 1 可以写成 A 的幂次和:特征多项式有如下形式
),则 A − 1 可以写成 A 的幂次和:特征多项式有如下形式
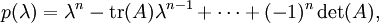
将方程式 p(A) = 0 同乘以 A − 1,便得到