價格彈性
出自 MBA智库百科(https://wiki.mbalib.com/)
價格彈性(price elasticity)
目錄 |
所謂價格彈性,即是需求量對價格的彈性,則指某一產品價格變動時,該種產品需求量相應變動的靈敏度。而價格彈性分析,就是應用彈性原理,就產品需求量對價格變動的反應程度進行分析、計算、預測、決策。
價格彈性表明供求對價格變動的依存關係,反映價格變動所引起的供求的相應的變動率,即供給量和需求量對價格信息的敏感程度,又稱供需價格彈性。商品本身的價格、消費者的收入、替代品價格,以及消費者的愛好等因素都會影響對商品消費的需求。價格彈性是指這些因素保持不變的情況下,該商品本身價格的變動引起的需求數量的變動。在需求有彈性的情況下,降價會引起購買量的相應增加,從而使消費者對這種商品的貨幣支出增加;反之,價格上升則會使消費者對這種商品的貨幣支出減少。在需求彈性等於1的情況下,降價不會引起消費者對這種商品的貨幣支出的變動。
價格彈性取決於該商品的替代品的數目及其相關聯(即可替代性)的程度、該商品在購買者預算中的重要性和該商品的用途等因素。價格彈性主要應用於企業的決策和政府的經濟決策。
價格彈性可分為需求價格彈性、供給的價格彈性、交叉價格彈性、預期價格彈性等各種類型。
需求價格彈性是需求變動率與引起其變動的價格變動率的比率,反映商品價格與市場消費容量的關係,表明價格升降時需求量的增減程度,通常用需求量變動的百分數與價格變動的百分數的比率來表示,也可做圖或列表示之;
供給價格彈性是供給變動率與引起其變動的價格變動率的比率,反映價格與生產量的關係,表明價格升降時供給量的增減程度,通常用供給量變動百分數與價格變動百分數的比率衡量;
交叉價格彈性又稱交錯價格彈性,是需求的變動率與替代品或補充品價格變動率的比率,表明某商品價格變動對另一商品需求量的影響程度;
預期價格彈性是價格預期變動率與引起這種變動的當前價格變動率的比率,反映未來價格變動對當前價格的影響,用預期的未來價格的相對變動與當前價格的相對變動的比例表示。
價格彈性的幾何理解[1]
對點彈性而言,不妨設需求曲線為Q=Q(P)。式中,P為價格,Q為需求量。此時設Ed表示價格彈性,則有
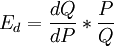
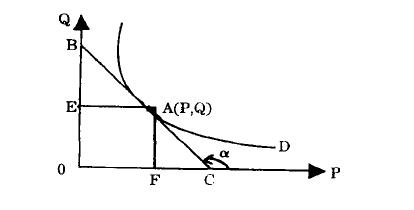
從圖中可知:D為需求曲線,其表達式為0=Q(P),點A的坐標為A(P,Q)
過A點的曲線D的切線斜率為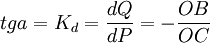 式中,Kd為切線的斜率。
式中,Kd為切線的斜率。
因為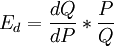 ,
,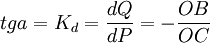 ,A點的坐標為P=AE,Q=AF,P=OE,Q=OF
,A點的坐標為P=AE,Q=AF,P=OE,Q=OF
所以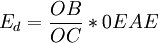
因為△BOS∽△BEA,所以, 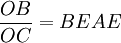
因為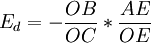 ,
,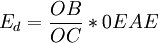 ,所以
,所以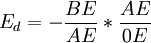
得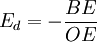
而且因為AE∥0C,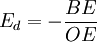 所以
所以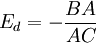 (平行切割)
(平行切割)
顯然,D線上任意一點處的彈性是以切點內分上部、下部線段的比值取負號。
價格彈性與斜率的關係及應用[1]
從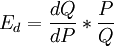 中看出,圖中A點切線的斜率是與Ed相關的,但不是同一種概念,即價格彈性不是斜率。
中看出,圖中A點切線的斜率是與Ed相關的,但不是同一種概念,即價格彈性不是斜率。
從圖中看,當切點位於切線中點時有:|Ed|=1
顯然,AB上|Ed|<1,AC上|Ed|>1。
這樣,即使是同一條需求曲線D上不同點處的價格彈性均不一樣。那麼,P處於何處時可降價呢?當價格P位於P>F且接近c的較高部位時,降價可使需求量Q增加;反之,當價格P位於P<F且接近0的較底部位時,降價對需求量的增加將不明顯,效果不會理想。
當不需計算Ed的精確值時,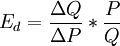 。這時應用可不必知道需求曲線方程即可不知Q=Q(P),只需知道需求曲線兩點的價格和需求量即可。
。這時應用可不必知道需求曲線方程即可不知Q=Q(P),只需知道需求曲線兩點的價格和需求量即可。
實例1:存線上性關係的某商店,即:Q=Q(P)是線性的。若價格由1元上升到3元,需求量由1000個單位下降到800個單位。求該商品的需求彈性。
解:由題意可得
△Q=800-1000=-200(單位)
△P=3-1=2(元)
Q=1000(單元) P=1(元)
則有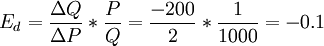
弧彈性公式的應用。
針對Q=Q(P),對P的上升/下降,|Ed|應一致,但基準量Q、P不同,|Ed|將不一致。
實例2:將實例1變化一下可得,P 由3元下降到1元,Q從800單位上升到1000單位,試求 。
解:△Q=1000-800=200(單元)
△P=1-3=-2(元)
Q=1000(單位)P=3(元)
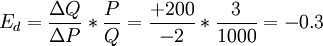
為了不出現上述現象,可用弧彈性公式來進行計算。 首先,看看公式的變化。
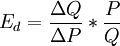
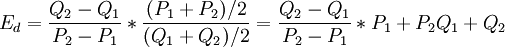
式中,Pl,Ql是基期數據;P2,Q2是報告期數據。這樣 便不再會出現P上升或下降的絕對量一致,Q 下降或上升的 絕對量一致, 不一致的問題。
實例3:
對實例1有
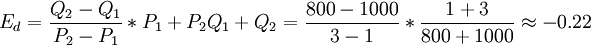
對實例2有
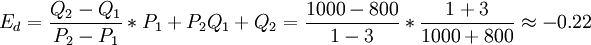
顯然,用弧彈性公式結果是一致的。
評論(共7條)
A點的坐標為P=AE,Q=AF,P=OE,Q=OF 這裡沒看懂
途中P是橫坐標 Q是縱坐標 那不應該是P=OF Q=OE嗎?
A點的坐標為P=AE,Q=AF,P=OE,Q=OF 這裡沒看懂
途中P是橫坐標 Q是縱坐標 那不應該是P=OF Q=OE嗎?
附上參考文獻,您可進行對比,希望對您有幫助哦~
你做錯叻!!!! 求變化的百分比 應該是(old-new)/new!!!!!!! 你全部都用的1000作為old的數值是不對的, 有時候從800變到1000, old=800 not 1000!!! 計算全有問題








很詳細,謝謝