ZETA评分模型

出自 MBA智库百科(https://wiki.mbalib.com/)

ZETA评分模型（Zeta Model）

　　1977年，阿尔特曼（Altman）、赫尔德门（Haldeman）和纳内亚南（Narayanan）对原始的Z-score模型进行扩展，建立了第二代模型。其目的是创建一种能够明确反映公司破产问题研究的最新进展的度量指标。因为破产公司的平均规模急剧增大，所以最近的研究大多集中在大型公司上，即破产前2年资产规模在$100百万的公司。所采用的数据：最近7年样本中53家破产公司中50家都破产了。分析过程中适当的做些调整使得模型可以在同样的基础上应用于零售业，这类企业尤其脆弱。另外，这个新的研究反映了财务报告标准以及会计实践方面的变化。同时，该模型还对从前模型构建中采用的统计判别技术进行了修正与精炼。

　　ZETA信用风险模型（ZETA Credit Risk Model）是继Z模型后的第二代信用评分模型 ，变量由原始模型的五个增加到了7个，适应范围更宽，对不良借款人的辨认精度也大大提高。

　　ZETA = ax₁ + bx₂ + cx₃ + dx₄ + ex₅ + fx₆ + gx₇

　　模型中的a、b、c、d、e、f、g，分别是无法获得ZETA模型中其变量各自的系数。x₁、x₂、x₃、x₄、x₅、x₆、x₇分别表示模型中的7个变量，7个变量是：资产收益率、收益稳定性指标 、债务偿付能力指标、累计盈利能力指标、流动性指标、资本化程度的指标、规模指标。

　　1.资产报酬率，采用税息前收益/总资产衡量。在以前的多变量研究中该变量表明评估公司业绩方面相当有效。

　　2.收入的稳定性，采用对X在5-10年估计值的标准误差指标作为这个变量的度量。收入上的变动会影响到公司风险，因此这种标准是相当有效的。

　　3.债务偿还，可以用人们所常用的利息保障倍数（覆盖率）即利税前收益/总利息偿付来度量，这是固定收益证券分析者和债券评级机构所采用的主要变量之一。

　　4.积累盈利，可以用公司的留存收益（资产减负债/总资产）来度量。该比率对于Z-score模型尤其有效，它需要考虑以下因素：公司年龄，公司股利政策，以及不同时期的获利记录。毫无疑问，不管是单变量法还是多变量法，该比率都是最重要的。

　　5.流动比率，可以用人们所熟悉的比率衡量。

　　6.资本化率，可以用普通股权益/总资本。在分子和分母中，普通股权益可以用公司五年的股票平均市场值衡量，而不是帐面值。五年平均市场值可以排除可能出现的严重、暂时性的市场波动，同时（与上述的X2）在模型中纳入了趋势的成分。

　　7.规模，可以用公司总资产的对数形式来度量。该变量可以根据财务报告的变动进行相应的调整。

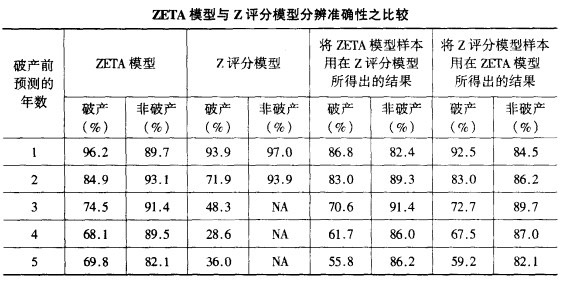
　　Altman等人曾对两者判别的准确性进行了比较，见下表：

　　ZETA评分模型改进的几个方面如下：

• 便利那个选择扩大了范围并进一步接近现实；

• 所选变量较前稳定；

• 在其样本的开发和统计技术方面都有大的改进；

• 比Z评分模型更为准确有效（特别是在破产之前，预测年限越长，则预测准确性就越高）。

　　1. 两个模型都依赖于财务报表的帐面数据，而忽视日益重要的各项资本市场指标，这就必然削弱预测结果的可靠性和及时性；

　　2. 由于模型缺乏对违约和违约风险的系统认识，理论基础比较薄弱，从而难以令人信服；

　　3. 两个模型都假设在解释变量中存在着线性关系，而现实的经济现象是非线性的，因而也削弱了预测结果的准确程度，使得违约模型不能精确地描述经济现实；

　　4. 两个模型都无法计量企业的表外信用风险，另外对某些特定行业的企业如公用企业、财务公司、新公司以及资源企业也不适用，因而它们的使用范围受到较大限制。

　　ZETA这种新模型在破产前5年即可有效地划分出将要破产的公司，其中破产前1年的准确度大于90%，破产前5年的准确度大于70%。新模型不仅适用于制造业，而且同样有效地适用于零售业。

　　依据在信用分析中的广泛使用的变量，首先选出了27个变量。这些变量可划分为获利能力度量指标、保障率与其它杠杆收益度量指标、流动能力度量指标、资本化比率度量指标、收益变动性指标等等。

　　对公司的财务报表数据所进行的最重要、最普遍的调整就是对租赁资本数据的调整，这也是运用这个模型对财务报告所作的唯一重大的调整。公司资产、负债需要再加上租赁资本总额，同时负债还要加上利息成本。当然对一些其它因素也需要进行相应的调整，如公积金、资产负债表的少数股权、不能合并的子公司收入, 商誉和无形资产以及资本化的研究和开发成本等因素。

　　1.信用政策。缺乏内部风险评分系统的机构可以通过ZETA的分值段与实际违约经验相结合的评分系统。ZETA等价评级（ZER）提供了处理不同区域、规模或所有权的客观且一致的方法。通过ZER结果与金融机构自己的评分结果相比较，可以分析一些异常现象以验证已给定的等级是否合适。

　　2.信用评审。随着借款者信用质量的提高或下降，这些模型能够为金融机构提供预先警告系统。

　　3.放贷。这些模型所提供的风险评估方法成本低而且速度快。通过利用分值与违约率之间的一致关系，可以在定价模型中考虑目标信用利差和意外损失。

　　4.证券化。由于它们提供了可靠而一致的信用语言，这些模型能够促进商业信贷的分层和结构化以实现证券化。实际上，这些模型是迎接90年代以后信用市场所面临的挑战的有效而严肃的方法。

　　ZETA评分模型的构建中的数理方法，综合以来，主要有以下几种：

　　1．判别分析法(discriminant analysis)

　　判别分析法(discriminant analysis，简称da ) 是根据观察到的一些统计数字特征，对客观事物进行分类，以确定事物的类别。它的特点是已经掌握了历史上每个类别的若干样本，总结出分类的规律性，建立判别公式。当遇到新的事物时，只要根据总结出来的判别公式，就能判别事物所属的类别。

　　da的关键就在于建立判别函数。目前，统计学建立判别函数常用方法有：一是未知总体分布情况下，根据个体到各个总体的距离进行判别的距离判别函数；二是已知总体分布的前提下求得平均误判概率最小的分类判别函数，也称距离判别函数，通常称为贝叶斯(bayes)判别函数；三是未知总体分布或未知总体分布函数前提下的根据费歇(fisher) 准则得到的最优线性判别函数。

　　2．多元判别分析法(multivariate discriminant analysis)

　　多元判别分析法(mda)是除美国外的其他国家使用最多的统计方法。多元线性判别分析法，可以具体为一般判别分析(不考虑变量筛选)和定量资料的逐步判别分析(考虑变量筛选)。但应用多元判别分析(mda)有三个主要假设：变量数据是正态分布的；各组的协方差是相同的；每组的均值向量、协方差矩阵、先验概率和误判代价是已知的。

　　该种方法的不足之处是必须建立在大量的、可靠的历史统计数据的基础之上，这在发展中国家如中国是难以具备的前提条件。

　　3．logit 分析判别方法

　　logit 分析与判别分析法的本质差异在于前者不要求满足正态分布或等方差, 从而消除了mda 模型的正态分布假定的局限性。其模型主要采用了logistic 函数。

　　该模型的问题在于当样本点存在完全分离时，模型参数的最大似然估计可能不存在，模型的有效性值得怀疑，因此在正态的情况下不满足其判别正确率高于判别分析法的结果。另外该方法对中间区域的判别敏感性较强，导致判别结果的不稳定。

　　4．神经网络分析法（artificial neural network，简称ann）

　　神经网络分析法是从神经心理学和认知科学研究成果出发，应用数学方法发展起来的一种具有高度并行计算能力、自学能力和容错能力的处理方法。它能有效解决非正态分布、非线性的信用评估问题，其结果介于0与1之间，在信用风险的衡量下，即为违约概率。神经网络分析方法应用于信用风险评估的优点在于其无严格的假设限制且具有处理非线性问题的能力。altman、marco和varetto（1994）在对意大利公司财务危机预测中应用了神经网络分析法；coats及fant（1993）trippi采用神经网络分析法分别对美国公司和银行财务危机进行预测，取得较好效果。然而，要得到一个较好的神经网络结构，需要人为随机调试，需要耗费大量人力和时间，加之该方法结论没有统计理论基础，解释性不强，所以应用受到很大限制。

　　5．聚类分析法(cluster analysis)

　　聚类分析(cluster analysis)属于非参数统计方法。信用风险分析中它根据由借款人的指标计算出的在样本空间的距离，将其分类。这种方法一个主要优点是不要求总体的具体分布；可对变量采用名义尺度，次序尺度，因此该方法可用于定量研究，也可对现实中的无法用数值精确表述的属性进行分析。这很适用于信用风险分析中按照定量指标(盈利比、速动比等) 和定性指标(管理水平、信用等级等) 对并不服从一定分布特性的数据信息分类的要求。例如，lundy运用该方法对消费贷款申请者的典型信用申请数据及年龄、职业、婚否、居住条件进行处理分成 6类并对每类回归评分，它不仅将借款人进行有效的分类而且帮助商业银行确定贷款方式策略。

　　6．k近邻判别法(k nearest neighbor)

　　k近邻判别法在一定距离概念下按照若干定量变量从样本中选取与确定向量距离最短k个样本为一组，适用于初始分布和数据采集范围限制较少时，减小了以函数形式表达内容的要求。另外，knn 通过将变量在样本整体范围内分为任意多决策区间，而近似样本分布。tametal将之用于信用风险分析，取马氏距离，从流动性、盈利性、资本质量角度选出的19 个变量指标，对样本分类，经比较其分类结果的准确性不如lda、lg以及神经网络。原因在于在同样的样本容量下，若对具体问题的确存在特定的参数模型并可能找出时，非参数方法不及参数模型效率高。

　　7．层次分析法（ahp）

　　该方法强调人的思维判断在决策过程中的作用，通过一定模式使决策思维过程规范化，它适用于定性与定量因素相结合、特别是定性因素起主导作用的问题，企业信用等级综合评价就是这种定性因素起主导作用的问题。ahp法的基本步骤是：建立递阶层次结构，构造判断矩阵，求此矩阵的最大特征根及其对应的特征向量，确定权重，并进行一致性检验。

　　8．其他方法

　　此外还存在着其他众多的方法：probit法、因子(logistic)法、模糊数学方法、混沌法及突变级数法、灰关联熵、主成分分析综合打分法、主成分分析与理想点的结合方法、原蚁群算法、数据包络判别法等等。关于这些方法的应用，将在后面的实证部分进行探讨。