肯德尔和谐系数
出自 MBA智库百科(https://wiki.mbalib.com/)
肯德尔和谐系数(the kandall coefficient of concordace)
目录 |
肯德尔和谐系数是计算多个等级变量相关程度的一种相关量。前述的spearman等级相关讨论的是两个等级变量的相关程度,用于评价时只适用于两个评分者评价N个人或N件作品,或同一个人先后两次评价N个人或N件作品,而kandall和谐系数则适用于数据资料是多列相关的等级资料,即可是k个评分者评(N)个对象,也可以是同一个人先后k次评N个对象。通过求得kandall和谐系数,可以较为客观地选择好的作品或好的评分者。
肯德尔和谐系数的公式与计算[1]
以下用W表示肯德尔和谐系数
(1)同一评价者无相同等级评定时,W的计算公式:
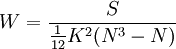 (1)
(1)
式中:N—被评的对象数; K—评分者人数或评分所依据的标准数;
S—每个被评对象所评等级之和Ri与所有这些和的平均数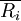 的离差平方和,即
的离差平方和,即
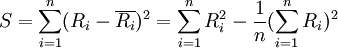
当评分者意见完全一致时,S取得最大值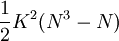 可见,和谐系数是实际求得的S与其最大可能取值的比值,故0≤W≤1。
可见,和谐系数是实际求得的S与其最大可能取值的比值,故0≤W≤1。
(2)同一评价者有相同等级评定时,W的计算公式:
![W=\frac{S}{\frac{1}{12}[K^2(N^3-N)-K\sum_{i=1}^K T_i]}](/w/images/math/d/c/b/dcb1e6ff8a53b302a1fdb1dc2315c3d2.png) (2)
(2)
式中K、N、S的意义同(1)式,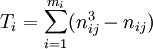
这里mi为第i个评价者的评定结果中有重复等级的个数,nij为第i个评价者的评定结果中第j个重复等级的相同等级数。
对于评定结果无相同等级的评价者,Ti = 0,因此只须对评定结果有相同等级的评价者计算Ti。
【例1】 某校开展学生小论文比赛,请6位教师对入选的6篇论文评定得奖等级,结果如下表所示,试计算6位教师评定结果的kandall和谐系数。
| 论文编号 评等 评分老师 | 一 | 二 | 三 | 四 | 五 | 六 | |
| A | 3 | 1 | 2 | 5 | 4 | 6 | |
| B | 2 | 1 | 3 | 4 | 5 | 6 | |
| C | 3 | 2 | 1 | 5 | 4 | 6 | |
| D | 4 | 1 | 2 | 6 | 3 | 5 | |
| E | 3 | 1 | 2 | 6 | 4 | 5 | |
| F | 4 | 2 | 1 | 5 | 3 | 6 | |
| Ri | 19 | 8 | 11 | 31 | 23 | 34 | 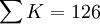
|
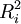 | 361 | 64 | 121 | 961 | 529 | 1156 | 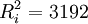
|
解:由于每个评分老师对6篇论文的评定都无相同的等级,故用公式(1),由表中数据得:
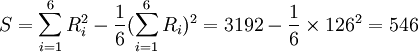
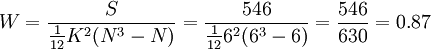
(由W=0.87表明6位老师的评定结果有较大的一致性)
【例2】 3名专家对6篇心理学论文的评分经等级转换如下表所示,试计算专家评定结果的肯德尔和谐系数
| 论文 等级 专家 | A | B | C | D | E | F | |
| 甲 | 1 | 4 | 2.5 | 5 | 6 | 2.5 | |
| 乙 | 2 | 3 | 1 | 5 | 6 | 4 | |
| 丙 | 1.5 | 3 | 1.5 | 4 | 5.5 | 5.5 | |
| Ri | 4.5 | 10 | 5 | 14 | 17.5 | 12 | 63 |
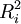 | 20.25 | 100 | 25 | 196 | 306.25 | 144 | 791.5 |
解:由于专家甲、丙对6篇论文有相同等级的评定,故用公式(2)计算W:
甲T = 23 − 2 = 6
丙T = (23 − 2) + (23 − 2) = 12
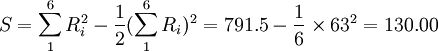
![W=\frac{S}{\frac{1}{12}[K^2(N^3-N)-K\sum T_i]}=\frac{130}{\frac{1}{12}[3^2(6^3-6)-3\times(6+12)]}=\frac{130}{153}=0.849673203=0.85](/w/images/math/1/d/e/1de22e9de9610bd1a179e8e4d219d8f4.png)
由W=0.85可看出专家评定结果有较大的一致性。
1、当评分者人数(k)在3-20之间,被评者(N)在3-7之间时,可查《肯德尔和谐系数(W)显著性临界值表》,检验W是否达到显著性水平。若实际计算的S值大于k、N相同的表内临界值 ,则W达到显著水平。
例如例3中,K=6 N=6,查表得检验水平分别为α = 0.01,α = 0.05的临界值各为S0.01 = 282.4,S0.05 = 221.4,均小于实算的S=546,故W达到显著水平,认为6位教师对6篇论文的评定相当一致。
2、当被评者n>7时,则可用如下的x2统计量对W是否达到显著水平作检验。
设H0:评价者意见不一致
则: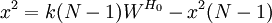 (3)
(3)
对给定的水平α,由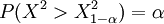 ,查df=N-1的X2分布表得临界值为分位数
,查df=N-1的X2分布表得临界值为分位数
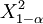 ,将计算出的kandall系数W等代入(3)式计算X2值
,将计算出的kandall系数W等代入(3)式计算X2值
若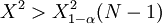 则拒绝H0,认为评分者的意见显著一致。
则拒绝H0,认为评分者的意见显著一致。
若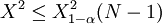 则H0认为评分者的评判显著不一致。
则H0认为评分者的评判显著不一致。
例如,在一次教学评价中,10位评价者对12项指示进行评价,已计算出W=0.65,需检验评价者的意见是否有显著的一致性(α = 0.01)。
将k=10 N=12 W=0.65代入(3)计算得
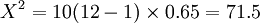
查表得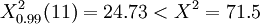
故认为10位评价者对12个指标的评价具有显著的一致性。
- ↑ 杨宗义.教育统计学[M].科学技术文献出版社,1990年08月第1版.
评论(共13条)
例2中S的计算有错误,应该为791-(63*63)/6=130
谢谢指正,已对相应内容做了修订。
MBA智库百科是大家可以参与编辑的百科,期待你的加入哦~
例2,Ti的计算,有点疑问,按照公式 好像分别是 6×6 和 12×12 啊
不好意思 好像是 甲T:6×6 丙T:6×6 + 6×6
给出的Ti值计算公式有误,应该把平方去掉。
下面的例子中计算是正确的,也就是没有算平方的。
谢谢指正,原文已修正!并附上参考文献,希望对您有帮助!
MBA智库百科是众人参与编辑和修改的百科,必然会造成一些不足,现已将参考文献添加,希望对你有帮助。








例2中S的计算有错误,应该为791-(63*63)/6=130