偏态分布
出自 MBA智库百科(https://wiki.mbalib.com/)
偏态分布(Skewed distribution)
目录 |
频数分布有正态分布和偏态分布之分。正态分布是指多数频数集中在中央位置,两端的频数分布大致对称。
偏态分布是指频数分布不对称,集中位置偏向一侧。若集中位置偏向数值小的一侧,称为正偏态分布;集中位置偏向数值大的一侧,称为负偏态分布。
偏态分布只有满足一定的条件(如样本例数够大等)才可以看做近似正态分布。
与正态分布相对而言,偏态分布有两个特点:
一是左右不对称(即所谓偏态);
二是当样本增大时,其均数趋向正态分布。
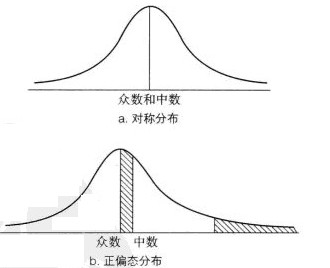
一个偏态分布的集中趋势[1]
当一个单峰分布呈很强的偏态形状时,你很难决定是否用中数还是均数代表分布的集中趋势(在这种情况下,众数也绝不可能是三者中最好的一个)。另一方面,对于图2a所示的对称单峰分布,均数和中数都十分精确地位于中央,众数也正位于此。因为分布是对称的,所以众数的两侧面积也相等。现在让我们来看看当加入几个高分数使得分布变成正偏态分布,情况会变成怎样(如图2b所示)。在右侧加入少量分数会使得右侧面积略微增加。为了使得两侧面积相等,中数必须往右移一点点。但是,请注意,中数并不需要沿着X轴移动太多。因为中数位于分布中比较厚的部分,所以只需往右稍移一点便足以弥补足够的面积给新加入的高分数(请看图2b中右端阴影部分是如何与中数和众数之间的阴影区域相等的)。可见,中数并不受到分布偏态的强烈影响,从而在描述分布的集中趋势方面很有优势。
图2 一个偏态分布的中数
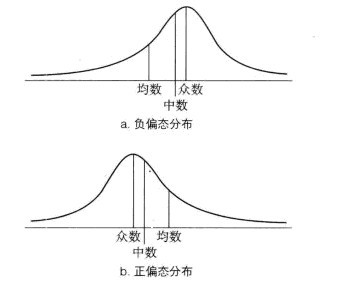
事实上,一旦你求出了一个分布的中数,则你可以取分布中任何一侧的一个分数,并将其移动远离中数。只要这个分数还是位于中数的其中一边,则你可以任意移动它到你想要的任何远的位置,中数都不会改变它原有的位置。但对于均数则不是这样了。均数会受到分布中任何一个分数的影响。因此,均数会被拉到偏态尾巴的方向,有时会被拉动很多,如图2所示。当分布呈负偏态时(图3a),均数会移至中数的左侧(即变得更负了),而对于正偏态的情况(图3b)则恰恰相反。反之,如果你同时有一个分布的均数和中数,而中数更高(即更正),那么该分布是负偏态;如果均数更高,那么该分布是正偏态。在一个正偏态分布中,超过一半的分数低于均数,而负偏态的情况则想反。如果均数和中数是相等的,则分布很可能是围绕中心对称的。
图3 一个偏态分布的均数
- ↑ (美)BARRY H. COHEN著;高定国等译.心理统计学.华东师范大学出版社









左偏分布图有点问题,不容易看出来