质量屋

用手机看条目

出自 MBA智库百科(https://wiki.mbalib.com/)

质量屋（the House of Quality）

什么是质量屋

　质量屋是由美国学者J．R．Hauser与D．C1ausing于1988年提出。“质量屋”是质量功能配置（QFD）的核心。

　　质量屋是一种确定顾客需求和相应产品或服务性能之间联系的图示方法。

　　质量屋（the House of Quality）一直是产品开发中连接用户需求与产品属性的经典工具。例如在一个相机产品开中，市场研究得到了用户对产品的若干需求，如，质量轻、使用方便、可靠、容易拿稳等等。通过市场人员与设计人员共同工作，确定实现不同需求可行的方式。这个过程同时排除掉了一些目前技术无法实现的需求，就像选择家具。一个完整的质量屋，还包括竞争对手表现、技术指标之间的关系、技术指标重要性得分等信息。

　　图1　质量屋图示

　　质量屋虽然是一个经典工具，但也只是一个基础工具，对复杂产品设计体系仍有局限。例如，该工具对于住宅产品来说并不是一个完美的工具。因为住宅产品不是一个简单属性的叠加，而是一个综合的解决方案。人们对房屋产品的整体的需求感受，驱动着人们对房屋各空间需求及其权衡取舍。这样，在住宅需求与住宅产品之间包含两层映射关系，一方面是整体的映射，另一方面是每个空间属性之间的映射。

　　以用户为中心的产品开发，建立在利用专业研究技术探求消费者心灵深处需求的基础上。这种需求是高度凝炼的，是一定时期内产品需要的原始驱动力。如果说研究用户的消费需求是对飘散的心灵电波的捕捉，建立营销语言和设计语言之间有效的对接，才能破译消费者心灵深处的密码，从而最终使需求信息在产品开发中发挥真正作用。

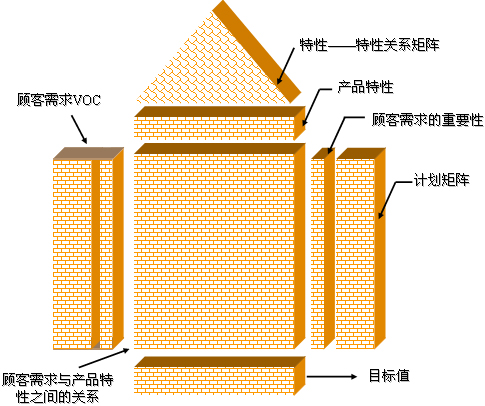
　　质量屋是一种直观的矩阵框架表达形式，是QFD方法的工具。建立质量屋的基本框架，给以输入信息，通过分析评价得到输出信息，从而实现一种需求转换。通常的质量屋如图1所示，其由以下几个广义矩阵部分组成：WHATS矩阵，表示需求什么；HOWS矩阵，表示针对需求怎样云做；相关关系矩阵，表示WHATS项的相关关系；HOWS的相互关系矩阵，表示HOWS阵内各项目的关联关系；评价矩阵，表示HOWS项的组织度或技术成本评价情况；竞争性或可竞争力或可行性分析比较。质量屋建立完成后，通过定性和定量分析得到输出项——HOWS项，即完成了“需求什么”到“怎样去做”的转换。

[编辑]

质量屋的组成

　　质量屋（HOQ）是驱动整个QFD(质量功能展开)过程的核心，它是一个大型的矩阵，由7个不同的部分组成（图1）。这7个组成部分分别是：

　　（1）顾客需求（customer requirements）。即VOC，通常它们可用亲密度图和树图表示。不同的产品有不同的顾客需求。例如，对于汽车来说，顾客需求可能是车门容易开启；对于银行来说，顾客需求可能是取款不用排队等。QFD就是用来部署（deploy）VOC的，而不是用来收集VOC的。收集VOC则是另一个相对独立的过程。

　　（2）产品特性（product features)。它们也可以用亲密度图和树图表示。产品特性是我们用以满足顾客需求的手段，产品特性也因产品不同而有差异。如对于车门，产品特性可能是关门所需的力量；对于割草机，产品特性可能是转动轴所需的推力。产品特性必须用标准化的表述。QFD中是利用顾客需求来产生产品特性的。

　　（3）顾客需求的重要性（importance of customer requirements）。我们不仅需要知道顾客需求些什么，还要知道这些需求对于顾客的重要程度。

　　（4）计划矩阵（planning matrix）。该矩阵包含一个对主要竞争对手产品的竞争性分析。矩阵中包括3列，分别代表对于现有产品所需的改进（改进率）、改进后可能增加的销售量（销售点）以及每个顾客需求的得分。

　　（5）顾客需求与产品特性之间的关系。这是矩阵的本体（中间部分），表示产品特性对各个顾客需求的贡献和影响程度。

　　（6）特性与特性之间的关系。一般地，一个特性的改变往往影响另一个特性。通常这种影响是负向的，即一个特性的改进往往导致另一个特性变坏。该特性关系图使我们能辨别这些特性之间的影响，以求得折衷方案。

　　（7）目标值。这是上述各部分对产品特性影响的结果。

[编辑]

QFD的工程应用过程概述

　　工程一一般的产品开发过程包括规划阶段、综合设计阶段、工艺阶段和生产计划阶段。在应用QFD方法时要先建立各阶段的质量屋，再进行需求变换，最后形成明确的生产要求，从而完成产品开发的质量功能配置的全过程。

　　QFD是一个跨专业的团队过程；

　　QFD是一种思想，一种产品开发和质量保证的方法论。它要求我们产品开发直接面向顾客需求，在产品设计阶段考虑工艺和制造问题，而质量屋则是在产品开发中具体实现这种方法论的工具；

　　QFD是一个非常结构化（structured)的、矩阵驱动（matrix-driven）的过程，其运行包括4个阶段：

将顾客需求(customer requirements)转化产品特性(performance measures)

将产品特性转化成零件特性(features and technology)

将零件特性转化成关键工艺操作(parts specification)

将关键工艺操作转化成生产要求(manufacturing processes)。

　　以下对各阶段质量屋的建立作论述以便于对质量屋概念的理解和对QFD系统的认识。

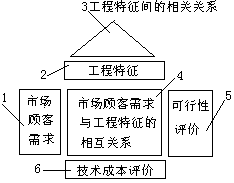
　　（1）产品规划阶段的质量屋　产品规划阶段的质量屋的构成形式如图2所示，其由下述几个部分组成。

　　图2　产品规划阶段的质量屋

　　第一部分是一个若干行一列的列阵，此列阵所反映的内容是市场顾客对产品的各种需求，（WHATS项）。这些市场顾客需求是通过对市场和顾客的需求将按过程驱动产品的QFD过程展开。市场顾客的需求是各种各样的，此项矩阵的建立应尽量充分、准确和合理，否则后续的所有需求变换工作者可能相对于真实的市场顾客需求而失真。就顾客的要求而言，亦有主次、轻重之分，QFD方法中对此的处理是：对市场顾客的各项需求给以权重因子以便进行排序，定义权重因子的总和为100％。注意，这里有顾客对象的权重区分，例如有主要客户对象和一般客户对象之分，显然不同客户需求的重要程度是不同的。也有同类市场顾客对产品的诸多质量功能要求排序时要注意避免重大的疏漏，亦要避免产品的冗余功能。这不工作是QFD实施成功的关键。

　　第二部分是一个一行若干列的行矩阵，是用来描述对应于市场顾客需求的工程特征要求，即有什么样的市场顾客需求就应有什么样的工程特征要求来对应保证。这种对应是多相关性的，市场顾客的某种需求可能对应着若干项工程特征要求，若干种工程特征要求有机结合才能满足某种市场顾客需求项。反过来讲，某种工程特征也可以同时满足若干项市场顾客的需求。工程特征要求是市场顾客需求的映射变换结果。

　　在以下论述中将会看到，这一阶段的工程特征要求将作为下一阶段质量屋的WHATS项。

　　第三部分称为质量屋的屋顶，在数学上是一个三角形矩阵，它表示的是工程特征之间的相关关系。从辩证法的观点来看，实现一个产品的诸多质量功能需求对应着诸多工程特征，各种市场顾客的质量功能需求之间有着相互关联影响，从而各种工程特征之间亦有着相互关联影响，某一种工程特征的改变会影响到其它工程特征跟着变化。为简化问题起见，在QFD技术中以三种形式来定性地描述工程特征之间的相关影响关系，即正相关（向相同方向变化）、不相关和负相关（向相反方向变化）。对相关程度还可以进一步地细分为强相关、一般相关和弱相关几种关系，并给以标度值来表达相关程度。据此可以对工程特征进行分析研究，发现各种工程特征之间可能存在的矛盾，由此重新进行设计，避免矛盾的产生。

　　第四部分是一个关系矩阵，该矩阵的行数与第一部分相同，列数与第二部分相同。表示各个工程特征项与各个币场顾客需求项的相互关系。各个项之间的错综复杂关系可以定量地给以分值来表示。一般分：强相关给九分，可理解成为了满足某种市扬顾客需求必需具备某种工程特征要求；一般相关给三分，可理解成为了满足某种市场顾客需求可以采用不同的工程特征与之对应；弱相关给一分，表示两项之间的关联关系很弱。利用关系矩阵可以明确工程特征与市场顾客需求间的对应关系。

　　第五部分是一个产品可行性评价矩阵，又称为市场评估矩阵，其行数与市场顾客需求矩阵相同，列数可以是一列，其中的内容表示要开发的产品针对各项市场顾客需求的竞争能力估价值。同时引人若干个市场上同类产品作为竞争对象进行比较，以判断产品的市场竞争力，由此在产品开发初期找出不足之处以进行调整改进。第六部分是产品规划阶段的技术和成本评估矩阵，其行列数与工程特征矩阵相对应，其中要建立的内容是各项工程特征的技术和成本评价数据，同时也建立若干个同类产品的相对应的数据信息进行分析对比，找出不足之处，提出改进措施。

　　这六个部分的矩阵构造完成后便形成了产品规划阶段的质量屋，这个质量屋的基本输入是市场顾客需求，针对需求的对策是一组工程特征需求，从而进行了需求变换。通过变换将市场顾客对产品的相对离散和模糊的需求变换为明确的工程特征要求。

　　在这一过程中会不可避免地产生各种矛盾冲突。例如有市场顾客对产品的各种要求的冲突，如质量和成本的冲突，功能间的冲突等；有工程特征间技术上的矛盾关系；还有与同类产品对比而产生的竞争力和技术成本的不协调问题等等。这些矛盾冲突是需要解决的，决定产品规划阶段质量屋的输出工作就是利用质量屋这种形式化的工具进行迭代分析来解决上述的矛盾冲突。对复杂的问题可以采用计算机辅助QFD过程。产品规划阶段质量屋的最终输出是工程特征要求列阵，通过实现工程特征要求来保证市场顾客的需求。

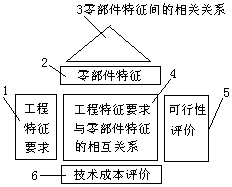
　　（2）零部件设计阶段的质量屋　工程特征需求的实现是由综合设计来保证的，在QFD方法中则还要建立体现综合设计内容的零部件设计阶段的质量屋。该阶段质量屋的构成形式与产品规划阶段的质量屋是类同的，如图3所示。　

　　图3　零部件设计阶段的质量屋

　　此阶段质量属的输入项（WHATS项）是产品的工程特征要求列阵（卜一阶段质量侵中力行矩阵，此处表示成列阵形式）。实现工程特征要求的对策是若干项零部件特征（HOWS项），以矩阵2来表示。矩阵3表示的是各种零部件特征间的相关性。同样，在工程特征要求矩阵和零部件特征矩阵之间存在的关系矩阵4表示相互关系。矩阵5是可行性评价矩阵，表示零部件特征对应于工程特征要求的可行性评价。矩阵6是技术评价矩阵，针对各项零部件特征进行技术和成本分析。

　　通过零部件设计阶段的质量屋的建立和分析，可以找出实现工程特征要求的难点和薄弱环节，重新进行有关零部件特征的方案设计。

　　零部件设计阶段的质量屋的最终输出是能保证实现工程特征要求的零部件特征要求。

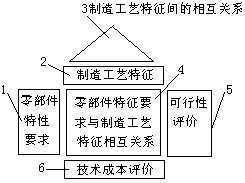
　　（3）工艺规划阶段的质量屋产品的零部件特征要求明确后，可以据此进行零部件的详细设计。为实现零部件特征要求，则要进行工艺规划设计，在QFD方法进程中对应的是工艺规划阶段质量屋的建立。该阶段的质量屋的内容如图4所示，质量屋的输入是零部件特征要求（质量屋的WHATS项）。输出是制造工艺特征要求（HOWS项）。通过这一过程完成产品的零部件设计要求向工艺流程设计的转换。

　　图4　工艺规划阶段的质量屋

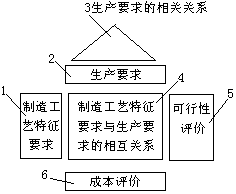
　　（4）生产计划阶段的质量屋工艺规划阶段质量屋的输出是制造工艺特征要求。为满足这些要求，要有生产计划安排以形成明确的生产要求。对应地建立QFD的生产计划阶段的质量屋，其形式如图5所示。此阶段质量屋的输入是产品的制造工艺特征要求，为实现制造工艺特征要求则要有明确的生产计划安排，在生产计划安排中包含诸多的生产要求。按这些要求就可以去组织产品的具体生产了。生产计划阶段质量屋的输出就是生产要求信息。

　　图5　生产计划阶段的质量屋

[编辑]

质量屋的案例分析

[编辑]

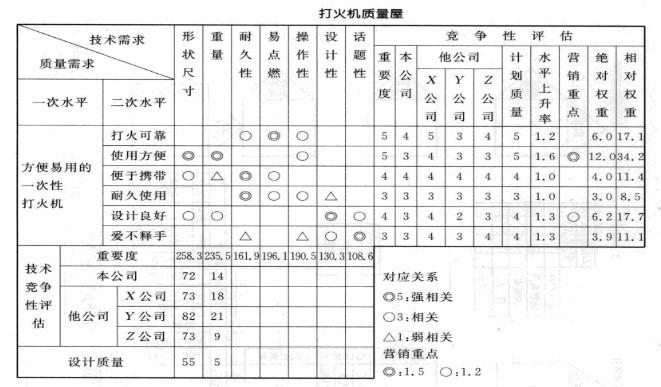
案例一：打火机质量屋实例^[1]

　　打火机是吸烟人士随身必带的物品之一。虽然昂贵.做工考究的名牌打火机因为体现出了一个人的身份和品味而备受青睐。但是方便易用的一次性打火机也因为其便宜.式样繁多的特性而受到人们的欢迎。然而。生产一次性打火机却面临很多问题。比如人们一般要求一次性打火机耐用(至少用光气体前不会坏)；在任何环境下都容易点着；最好样式也多一些。能够引起别人的注意。但具体生产的时候。一来不清楚各个顾客要求和生产有什么联系。二来各个指标的权重分配也成问题。因此。在进行一次性打火机的设计和生产过程里。使用了以质量屋矩阵为核心的QFD。最终。顾客的需求转变成产品的技术特性。并在生产过程中得到很好的支撑。

　　本例中。我们详细描述了如何构造打火机的质量屋。

　　(1)顾客需求

　　①顾客需求的获取

　　能否及时地获取顾客需求即顾客的声音(Voice 0f Customer，VOC)以及所获取的顾客需求是否全面、详尽、真实。是成功实施和应用QFD的基础。我们必须科学地选择所要调查的对象.调查的方法以及后面的分析方法。这样，在调查完成之后。我们才能最忠实地保持顾客声音的原貌。

　　对于一次性打火机的用户资料的收集。首先。我们考虑到一次性打火机的使用者(吸烟人士)一般都是中青年的男性。也就是15～35岁的男子。这个阶段的男子考虑打火机的方便使用，款式时尚、更换容易、价格低廉等特性的多些。因此是一次性打火机的主要消费者。那么调查的时候。就要尽可能的在这个年龄范围内进行。至于职业.地域分布倒是可以考虑的少些。

　　另外。在进行调查的时候。考虑到地域可能分布较广。可以采用邮寄问卷的方法。虽然该方法可能回收期长些。回收率也不是太高。但其低廉的费用还是比较适合大范围的调查的。下表是设计的调查用表样例。

　　通过以上的调查。将会得到很庞大的顾客需求的资料。由于调查对象的文字描述的模糊性和语言风格的特异性。有必要对上述资料进行整理和分析。提取出相同的元素或项目。

　　②顾客需求的分析和整理

　　收集到的顾客需求是各种各样的。有要求.意见.抱怨.评价和希望。有关于质量的。有涉及功能的。还有涉及价格的。所以必须对从用户那里收集到的情报进行分类.整理。通过对调查信息的分析与整理。形成QFD配置所需的顾客需求信息及形式。一般我们通过下面几个步骤来实现这个转化过程。

　　③概括合并顾客需求

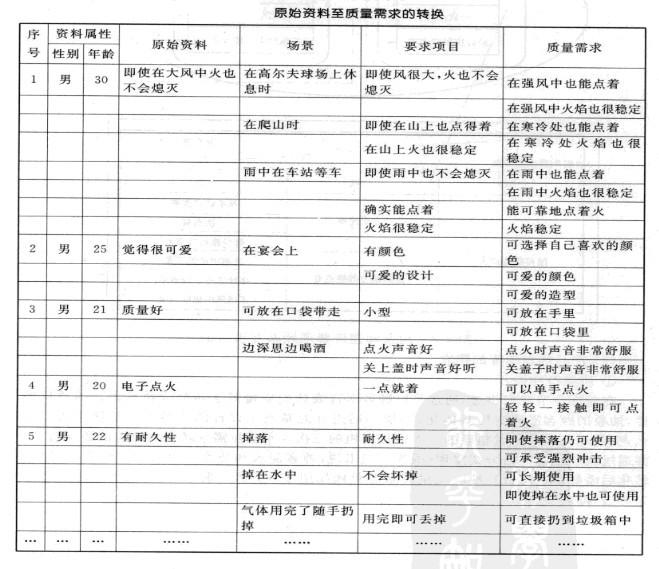
　　顾客对其需求的描述经常很长。为了便于在QFD矩阵中输入。必须对它们进行概括。在用简洁明了的语言概括顾客需求后。应将表达同一含义或相似含义的顾客需求进行合并。一般来说。总顾客需求数目最好控制在25个以下。最多不要超过50个。

　　a.将原始资料变换成顾客的质量需求一般。先将原始资料变换成为要求项目。然后再将要求项目转换为质量需求。注意在第一步变换中。最好能在不同的场景下考虑以便引出比较具体的要求项目。而在由要求项目向质量需求转换时。要注意语言的简洁.形象.具体和准确。每一项质量需求不要包含两个以上方面的内容。

　　在本例中。我们将收集的资料进行适当排列。并针对每一个调查对象。进行一定的换位思考和场景联想。力争真正理解调查对象的需求。最后对得出的要求项目和质量需求进行整理。原始资料至质量需求的转换如下表所示。

　　b.质量需求的分类与展开

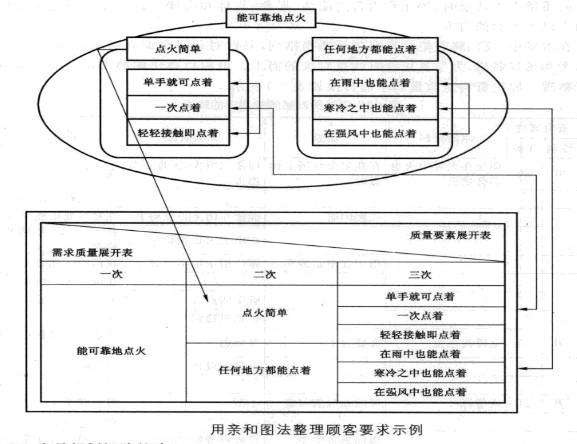
　　上述整理后的顾客需求是随意排列的。且存在重复和条理性不强等问题。对它们合理的分类有助于QFD矩阵的方便构造。我们采用第三章讲过的亲和图法对顾客需求进行分类。

　　以“能可靠地点火”这一质量需求为例。列示了其中隐含的下层水平质量需求。用亲和图法整理顾客需求示例如图4—8所示。

　　(2)产品规划矩阵的建立

　　①质量特性展开

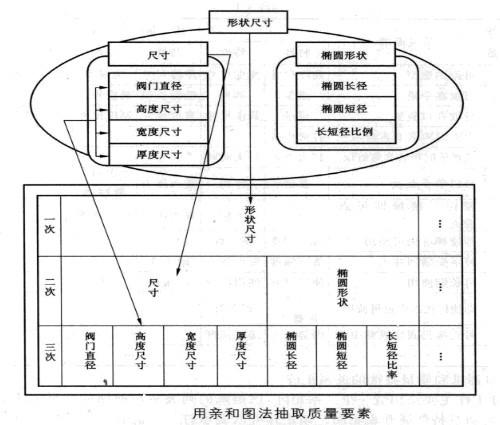
　　在前面章节我们讲过。通过将以顾客语言表达的质量需求转换成技术语言的质量特性。抽象的顾客需要变得具体化。并能够通过在此基础上设计的产品得以最终实现。那么。我们也可以把经过整理的一次性打火机的三次水平质量需求转化为对应的质量特性。并通过亲和图法进行分类整理(因为一般来说。顾客需求和技术需求之间存在着交叉性。转化后需要整理综合)。抽取质量要素的示例如下图所示。最终。我们也可以得到一个矩阵表。即如下表。

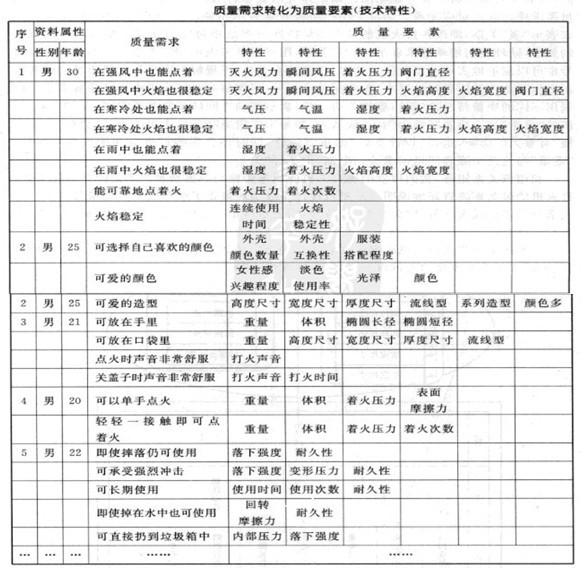
　　②质量需求和质量特性的关系矩阵

　　这部分工作主要是构造一个关系矩阵。该矩阵的列表头与前面的质量需求展开表相同。行表头与质量特性展开表相同。该矩阵可以表示打火机的各个质量特性项与各个质量需求项之间的对应关系。通常采用一组符号来表示相关程度的差异。例如。用双圆圈来表示“强”关系。即改善打火机的某个质量特性与满足相对应的顾客质量需求有比较强的关系。同理我们用单圆来表示“中等”关系。用三角形来表示“弱”关系。一组相关程度符号也可以定量地表示一组分值。这里。强相关给五分。可理解为满足打火机市场的顾客需求必须具备这种质量特性要求；中等相关给三分。可理解为对打火机市场的顾客需求可以采用不同的质量特性来满足；弱相关给一分。表示两项之间的关联关系很弱。例如以打火机的“重量”这一质量特性为例。一般认为。如果采取措施降低打火机的重量。会对“使用方便”有重大的影响。也是“设计良好”的重要条件。同时还会影响打火机的便携性。因此。“重量”与这两个顾客质量需求分别呈强、中、弱的关系。

　　利用该关系矩阵。我们可以明确打火机的质量特性与顾客质量需求之间的对应关系。打火机的关系矩阵直观地说明了质量特性是否适当地覆盖了顾客需求。如果关系矩阵中关系符号很少或大部分是“关系微弱”符号。则表示质量特性没有足够地满足顾客需求。应对它进行修改。

　　按上述步骤构造打火机质量屋如表4-11所示。在质量设计中。质量要素很多的情况下。可以选择重要度高的进行重点设计。如本例中的“形状尺寸”和“重量”。

[编辑]

案例二:基于质量屋矩阵的产品模块划分方法^[2]

　　基于HOQ矩阵的两阶段分组方法,根据HOQ图中的用户需求与工程性能关系矩阵以及工程性能之间的互相关矩阵的不同特点,采用不同的分组策略,实现对用户需求以及产品工程性能的分组,从而实现产品的模块划分以及对HOQ矩阵的分解。

　　1.用户需求与工程性能的HOQ图的建立

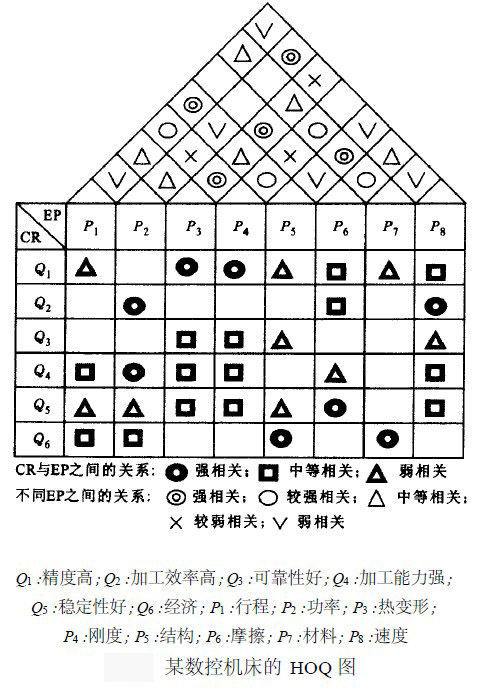
　　HOQ图一般由7个部分组成,本文对其进行了简化,仅对其中的用户需求(CR)与工程性能(EP)的关系矩阵R,以及工程性能(EP)之间互相关矩阵C的组成进行讨论.R中的关系系数 $r i j$ 表示了用户需求 $Q i$ 与工程性能 $P j$ 之间关系的强度,若 $Q i$ 与 $P j$ 之间没有联系,则相应项保持空项,即表示 $r i j = 0$ .相似地对于C,用互相关系数 $c i j$ 表示 $P i$ 与 $P j$ 之间关系的强度.目前,有多种确定 $r i j$ 和 $c i j$ 值的方法,如层次分析法(AHP)等.下图所示是一个经过简化的某机床用户需求与工程性能的HOQ图。

　　2.基于互相关矩阵的工程性能EP的分组

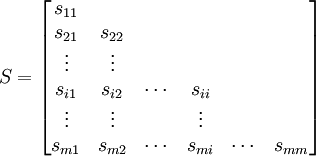
　　HOQ的EP互相关矩阵反映了工程性能彼此之间的耦合关系或约束关系,对EP分组就是在EP互相关矩阵的基础上,将EP分解为彼此间具有紧密联系,而各组间具有较少耦合的几组。可以采用元素间的距离d或元素的相似度s作为对元素分组的标准,并将距离较短或相似度较大的2个元素归为一组.根据EP的互相关矩阵按以下方法得到EP的距离矩阵。

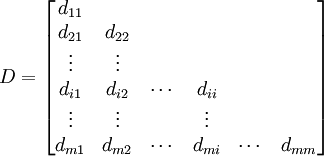
　　 $D=\begin{bmatrix} d_{11} \\ d_{21} & d_{22} \\ \vdots & \vdots \\ d_{i1} & d_{i2} & \cdots & d_{ii}\\ \vdots & \vdots & &\vdots \\ d_{m1}& d_{m2} & \cdots & d_{mi} & \cdots & d_{mm}\end{bmatrix}$

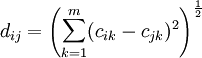　　 $d_{ij}=\left(\sum^m_{k=1}(c_{ik}-c_{jk})^2\right)^{\frac{1}{2}}$ 　　( $i\ne j$ )

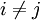　　式中： $d i i = 0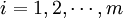$ ( $i=1,2,\cdots,m$ ). $c i k$ 、 $c j k$ 是EP互相关矩阵的元素,即 $P k$ 与 $P i$ 、 $P j$ 的互相关系数.由于D为一对称矩阵,因此式中仅列出了其下三角的元素.由D可以得到EP的相似度矩阵。

　　 $S=\begin{bmatrix} s_{11} \\ s_{21} & s_{22} \\ \vdots & \vdots \\ s_{i1} & s_{i2} & \cdots & s_{ii} \\ \vdots & \vdots & & \vdots \\ s_{m1} & s_{m2} & \cdots & s_{mi} & \cdots & s_{mm}\end{bmatrix}$

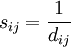　　 $s_{ij}=\frac{1}{d_{ij}}$ 　　( $i\ne j$ )

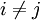　　式中： $s i j = m a x (s i j)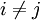$ ( $i\ne j$ )。对EP的分组可采用传统的层次分组算法,如SL(Single Linkage)、AL(Average Linkage)、CL(Complete Linkage)等.MMC(Min-Max Cut)是Ding等所提出的一种用于图像划分和数据融合的方法,该方法可将图像划分问题转换为对Fiedler特征值及其对应的特征向量的求解.本文将最大-最小(MMC)方法用于实现对EP的分组,在对EP分组时,必须遵守以下原则:①不同组之间元素的距离应尽可能大或它们的相似度应尽可能小;②同一组元素之间的距离应尽可能小或它们的相似度尽可能大.采用相似度作为EP分组的依据.假设有 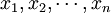$x_1,x_2,\cdots,x_n$ 共n个元素,将其分为两大组( $C 1$ 和 $C 2$ ),则条件①为

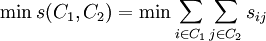
　　 $\min s(C_1, C_2)=\min\sum_{i\in C_1}\sum_{j\in C_2} s_{ij}$

　　条件②为

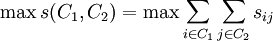
　　 $\max s(C_1, C_2)=\max\sum_{i\in C_1}\sum_{j\in C_2} s_{ij}$

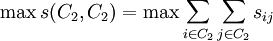
　　 $\max s(C_2, C_2)=\max\sum_{i\in C_2}\sum_{j\in C_2} s_{ij}$

　　式中: $s i j$ 是元素 $x i$ 和 $x j$ 的相似度.根据MMC方法,以上两个条件可转化为如下的目标函数。

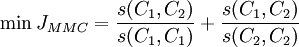　　 $\min J_{MMC}=\frac{s(C_1,C_2)}{s(C_1,C_1)}+\frac{s(C_1,C_2)}{s(C_2,C_2)}$ 　　(1)

　　式(1)可通过下式求得最小值:

　　 $(W - S) q = λ W q$ 　　(2)

　　式中:W是一对角阵,其元素为

w i i = \sum s i j j

;q表示指示向量;

λ

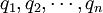是特征值.求解式(2)的次小特征值所对应的特征向量(Fiedler向量),该向量的分量分别为 $q_1,q_2,\cdots,q_n$ ，若某个分量

q i > 0

,则它所对应的项

x i

属于

C 1

组,否则

x i

属于

C 2

组.由此可将元素分为两组,如果要继续分组,可选择其中一组作为分组对象,选择的原则是具有最大平均距离的组,即使目标函数

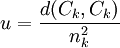
　　 $u=\frac{d(C_k,C_k)}{n_k^2}$

　　最大的 $C k$ 组为下一个分组对象,其中

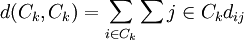
　　 $d(C_k,C_k)=\sum_{i\in C_k}\sum{j\in C_k} d_{ij}$

　　式中: $n k$ 是 $C k$ 中元素的个数. 再按max-min方法对其进行分组,由此可以得到多个分组方案.以平均损失度作为评判各分组方案优劣的依据,即

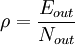
　　 $\rho=\frac{E_{out}}{N_{out}}$

　　式中: $E o u t$ 为C中位于各方块阵外的所有相关系数 $c i j$ 之和; $N o u t$ 为C中位于各方块阵外所有单元的个数,即

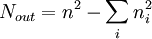
　　 $N_{out}=n^2-\sum_i n^2_i$

　　为使 $ρ$ 为最小时所对应的分组情况为最优分组方案,可将EP分为p组,分别为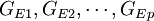 $G_{E1},G_{E2},\cdots,G_{Ep}$ 。

　　3.CR与EP的关系矩阵分解

　　对EP分组的基础上, 按照以下2个原则对CR与EP的关系矩阵R进行分解:①惟一原则; ②满意度最大原则. 原则①表示每个CR与EP只惟一地属于某一模块,原则②要求分解得到模块的r元素总和为最大. 因此,首先将R转化为CR与工程性能组GE的关系矩阵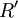 $R^\prime$ ,其元素

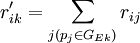
　　 $r^\prime_{ik}=\sum_{j(p_j\in G_{Ek})}r_{ij}$

　　如下表所示，将对R的分解问题转化为在同时满足原则①和②的条件下,根据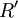 $R^\prime$ 将CR划分为p组的问题.

　　　用户需求与工程性能组的 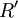$R^\prime$ 矩阵

用户需求	工程性能组
用户需求	$G E 1$	$G E 2$	$\cdots$	$G E k$	$\cdots$	$G E p$
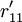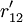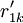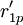
$Q 1$	$r^\prime_{11}$	$r^\prime_{12}$	$\cdots$	$r^\prime_{1k}$	$\cdots$	$r^\prime_{1p}$
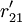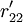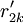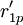
$Q 2$	$r^\prime_{21}$	$r^\prime_{22}$	$\cdots$	$r^\prime_{2k}$	$\cdots$	$r^\prime_{1p}$
$\vdots$	$\vdots$	$\vdots$		$\vdots$		$\vdots$
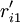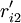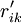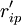
$Q i$	$r^\prime_{i1}$	$r^\prime_{i2}$	$\cdots$	$r^\prime_{ik}$	$\cdots$	$r^\prime_{ip}$
$\vdots$	$\vdots$	$\vdots$		$\vdots$		$\vdots$
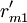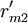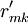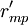
$Q m$	$r^\prime_{m1}$	$r^\prime_{m2}$	$\cdots$	$r^\prime_{mk}$	$\cdots$	$r^\prime_{mp}$

　　定义变量

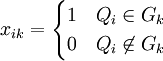　　 $x_{ik}=\begin{cases} 1 & Q_i \in G_k \\ 0 & Q_i\not\in G_k \end{cases}$ 　　(3)

　　按照原则①, $x i k$ 应满足关系

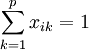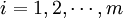　　 $\sum^p_{k=1}x_{ik}=1$ 　　( $i=1,2,\cdots,m$ )　　(4)

　　提出目标函数

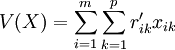　　 $V(X)=\sum^m_{i=1}\sum^p_{k=1}r^\prime_{ik}x_{ik}$ 　　(5)

　　原则②可转化为 $max V (X)$ ,则对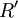 $R^\prime$ (即对R)的分解可转换为在满足约束式(3)、(4)的条件下,使式(5)最大化的优化问题,即一个带约束的0-1整型优化问题.因此,可采用多种方法,如穷举法、遗传算法等,来求解该优化问题。

　　4.应用实例

　　以上图所示的某数控机床的用户需求与工程性能HOQ图为例,用户需求CR与工程性能EP之间的关系用弱(1),中等(3),强(9)来表示,工程性能EP之间的关系用弱(011),较弱(013),中等(015),较强(017),强(019)来表示.由此得到与EP有关的矩阵为。

　　C= $\begin{bmatrix}1&0.1&0.5&0.7&0.9&0&0.5&0.1\\0.1&1&0.5&0.3&0.1&0&0&0.9\\0.5&0.5&1&0.9&0.5&0.9&0.5&0.3\\0.7&0.3&0.9&1&0.7&0.3&0.7&0\\0.9&0.1&0.5&0.7&1&0.1&0.9&0.1\\0&0&0.9&0.3&0.1&1&0.7&0.5\\0.5&0&0.5&0.7&0.9&0.7&1&0.1\\0.1&0.9&0.3&0&0.1&0.5&0.1&1\end{bmatrix}$

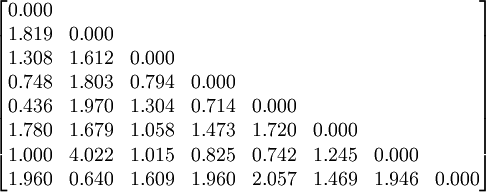
　　D= $\begin{bmatrix}0.000\\1.819&0.000\\1.308&1.612&0.000\\0.748&1.803&0.794&0.000\\0.436&1.970&1.304&0.714&0.000\\1.780&1.679&1.058&1.473&1.720&0.000\\1.000&4.022&1.015&0.825&0.742&1.245&0.000\\1.960&0.640&1.609&1.960&2.057&1.469&1.946&0.000\end{bmatrix}$

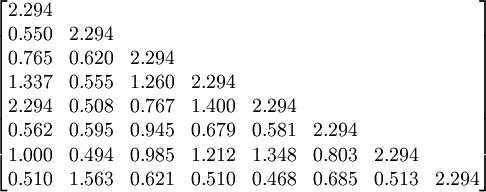
　　S= $\begin{bmatrix}2.294\\0.550&2.294\\0.765&0.620&2.294\\1.337&0.555&1.260&2.294\\2.294&0.508&0.767&1.400&2.294\\0.562&0.595&0.945&0.679&0.581&2.294\\1.000&0.494&0.985&1.212&1.348&0.803&2.294\\0.510&1.563&0.621&0.510&0.468&0.685&0.513&2.294\end{bmatrix}$

　　式(2)的次小特征值为01568,它所对应的特征向量(Fiedler向量)为(01285,-01596,010361,01212,01303,-01126,01195,-01609),因此可将EP分为 $G E 1 = (P 1, P 3, P 4, P 5, P 7)$ , $G E 2 = (P 2, P 6, P 8)$ ,Nout=30, $ρ 1 = 0.247$ 。由于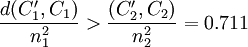 $\frac{d(C^\prime_1,C_1)}{n^2_1}>\frac{(C^\prime_2,C_2)}{n^2_2}=0.711$

　　因此选择P_2、P_6和P_8分为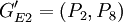 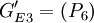$G^\prime_{E2}=(P_2,P_8)$ , $G^\prime_{E3}=(P_6)$ 两组，此时\Nout=3, $ρ 2 = 0.241$ 。由于 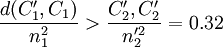$\frac{d(C^\prime_1,C_1)}{n^2_1}>\frac{C^\prime_2,C^\prime_2}{n^{\prime2}_2}=0.32$ ，因此选择P_1、P_3、P_4、P_5、和P_7、作为下一组分组对象,可分为G^\prime_{E1}=(P_1,P_5), 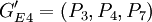$G^\prime_{E4}=(P_3,P_4,P_7)$ ,此时Nout=46,\rho_3=0.343.由于

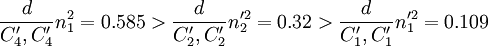　　 $\frac d{C^\prime_4,C^\prime_4}{n^2_1}=0.585>\frac d{C^\prime_2,C^\prime_2}{n^{\prime2}_2}=0.32>\frac d{C^\prime_1,C^\prime_1}{n^{\prime2}_1}=0.109$ 。

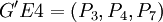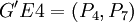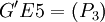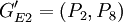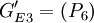　　因此再次选择 $G^\prime{E4}=(P_3,P_4,P_7)$ 作为分组对象,可将其分为 $G^\prime{E4}=(P_4,P_7)$ 和 $G^\prime{E5}=(P_3)$ ，此时Nout=50, $ρ 4 = 0.372$ .由于 $ρ 2$ 最小，因此选择它所对应的分组情况作为分组结果，即将所有EP分为 $G E 1 = (P 1, P 3, P 4, P 5, P 7)$ 、 $G^\prime_{E2}=(P_2,P_8)$ 和 $G^\prime_{E3}=(P_6)$ 3个组.由此得到CR与工程性能组的关系矩阵 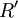$R^\prime$ ,如表所示

　　　某数控机床用户需求与工程性能组的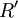 $R^\prime$ 矩阵

用户需求	工程性能组
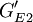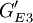
用户需求	$G E 1$	$G^\prime_{E2}$	$G^\prime_{E3}$
$Q 1$	21	3	3
$Q 2$	0	18	3
$Q 3$	7	1	0
$Q 4$	7	1	0
$Q 5$	8	4	9
$Q 6$	21	3	0

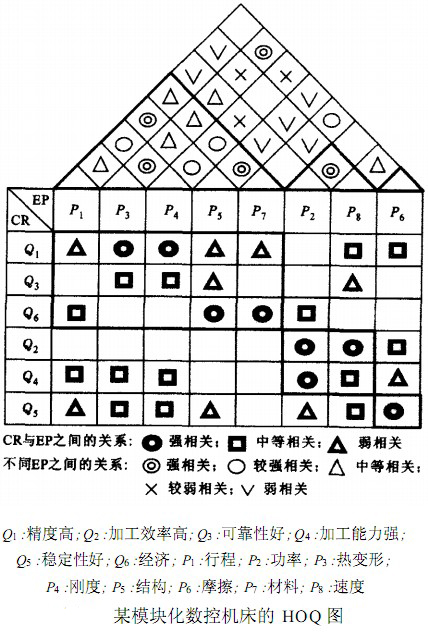
　　　采用遗传算法,求解式(3)～式(5),得到 $G 1 = (Q 1, Q 3, Q 6, G E 1) = (Q 1, Q 3, Q 6, P 1, P 3, P 4, P 5, P 7)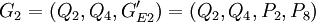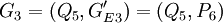$ , $G_2=(Q_2,Q_4,G^\prime_{E2})=(Q_2,Q_4,P_2,P_8)$ , $G_3=(Q_5,G^\prime_{E3})=(Q_5,P_6)$ ,此时 $max$ V(x)=88

　　分块后的HOQ矩阵如下图所示,其中第1组( $G 1$ )包括了行程、热变形、刚度、结构、材料等工程性能,它们都涉及到机床的结构特性.由于机床的结构在很大程度上取决于其材料和行程,因此它们之间具有较大的耦合系数,而机床刚度和行程、材料以及热变形也是相互紧密联系的,因此将行程、热变形、刚度、结构、材料等归为一组是合理的.与之相关的用户需求是机床的精度、可靠性和经济性,这些用户需求都需要通过机床结构、材料、行程、刚度、热变形等工程性能加以实现,因此它们之间具有紧密的联系,在设计中可以作为一个模块来考虑。第2组( $G 2$ )包括了功率和速度,它们反映了机床的运动学特性,与机床的速度和功率紧密相关,主要用于满足用户对机床的加工效率与加工能力的需求,因此将其归为一组也是合理的。第3组( $G 3$ )只包括摩擦虽然它与机床材料以及热变形都有关系,但与第1组的其他工程性能之间联系并不大,故将摩擦特性单独列出。摩擦在很大程度上影响着机床的稳定性因此将摩擦和机床的稳定性作为一个模块。由于模块划分结果与实际状况相符,因此证明了本文基于HOQ矩阵的两阶段产品模块化分组方法的有效性。

　　互相关矩阵为基础,通过将其转化为工程性能的相似度矩阵,借助max-min分组方法,将复杂的分组问题转化为可由计算机处理的Fiedler特征值及其特征向量的求解问题,并以平均损失度作为分组优劣的依据,实现对工程性能的分组.在得到分组数的条件下,再以用户需求与工程性能的关系矩阵为基础,通过求解简单的0-1整型规划问题实现对用户需求的分组.通过对某机床设计的运行实例表明,采用本文的方法可得到较为合理的产品设计模块划分,从而为从HOQ矩阵出发实现机械产品模块化的概念设计,以及将复杂的设计问题进行简化提供了工具。

[编辑]

参考文献

↑ 熊伟,丁伟儒著.第四章质量机能展开软件质量管理新模式.中国标准出版社,2008.5.第77页
↑ 孙挪刚梅雪松张优云.基于质量屋矩阵的产品模块划分方法.西安交通大学学报.2006年1月第40卷第1期

来自"https://wiki.mbalib.com/wiki/%E8%B4%A8%E9%87%8F%E5%B1%8B"

打开MBA智库App, 阅读完整内容打开App

如果您认为本条目还有待完善，需要补充新内容或修改错误内容，请编辑条目或投诉举报。

本条目由以下用户参与贡献

Angle Roh,Wwdz,Kuxiaoxue,Cabbage,Vulture,Zfj3000,Dinging,Dan,Yixi,鲈鱼,KAER,方小莉,寒曦.

页面分类: 质量管理工具

评论(共21条)

提示:评论内容为网友针对条目"质量屋"展开的讨论，与本站观点立场无关。

125.94.198.* 在 2008年10月6日 21:34 发表

写得很好

回复评论

116.10.196.* 在 2009年4月9日 11:50 发表

不错，受教育了

回复评论

219.239.98.* 在 2009年6月15日 09:44 发表

这个名词是谁提出的？什么年代提出的？

回复评论

60.30.66.* 在 2009年10月22日 19:26 发表

有改进方式吗？毕竟不适合大型系统的应用

回复评论

111.225.123.* 在 2010年5月9日 21:57 发表

不错，有没有将零部件特征，转化成工艺特征的案例呀

回复评论

64.246.212.* 在 2010年7月26日 08:28 发表

看起来有点晕，楼上都是高人

回复评论

Gombalib (Talk | 贡献) 在 2010年10月14日 15:05 发表

产品太大，或者说功能太多了，这个方法用起来就费劲了吧，关键属性觉得用这些方法还是觉得可以。

回复评论

Gombalib (Talk | 贡献) 在 2010年10月14日 15:28 发表

典型的日本人的做法，小而精，到不一定能实现。

回复评论

218.66.14.* 在 2011年1月12日 22:26 发表

各种大神啊···

回复评论

58.250.81.* 在 2011年3月11日 16:35 发表

案例看不明白

回复评论

Dan (Talk | 贡献) 在 2011年3月12日 11:24 发表

58.250.81.* 在 2011年3月11日 16:35 发表

案例看不明白

增加了一个新的案例，希望对你有帮助！

回复评论

113.16.175.* 在 2011年4月29日 17:12 发表

219.239.98.* 在 2009年6月15日 09:44 发表

这个名词是谁提出的？什么年代提出的？

美国学者Hauser和Clausing于1988年提出的

回复评论

Anenie (Talk | 贡献) 在 2011年4月29日 17:15 发表

Gombalib (Talk | 贡献) 在 2010年10月14日 15:05 发表

产品太大，或者说功能太多了，这个方法用起来就费劲了吧，关键属性觉得用这些方法还是觉得可以。

我认为正是大规模的产品才适用这种方法，小产品可以通过复用解决。功能多时利用质量屋可以很好的跟踪管理，而至于方法本身，完全可通过计算机辅助解决。

回复评论

Anenie (Talk | 贡献) 在 2011年4月29日 17:17 发表

60.30.66.* 在 2009年10月22日 19:26 发表

有改进方式吗？毕竟不适合大型系统的应用

可以结合数量化理论3类，模糊层次分析法，信息熵等方法进行优化。个人认为非常适合大型系统，反倒不适合小型系统。

回复评论

Anenie (Talk | 贡献) 在 2011年4月29日 17:20 发表

113.16.175.* 在 2011年4月29日 17:12 发表

美国学者Hauser和Clausing于1988年提出的

详见1988年哈佛商业评论上的著名论文《The House of Quality》，具有划时代的意义。

回复评论

118.251.183.* 在 2011年6月13日 01:09 发表

对于服务类行业如果用质量屋的形式应该怎么样去表现出来

回复评论

118.251.183.* 在 2011年6月13日 01:11 发表

是基于服务业的质量管理过程

回复评论

221.11.20.* 在 2014年4月24日 13:48 发表

案例中的重要度权重等那些的具体数据都是怎么得到的

回复评论

赵紫妤VIP (Talk | 贡献) 在 2017年6月24日 11:40 发表

这个真的很有用。

回复评论

59.33.93.* 在 2019年3月19日 13:34 发表

Dan (Talk | 贡献) 在 2011年3月12日 11:24 发表

增加了一个新的案例，希望对你有帮助！

很详细

回复评论

154.86.159.* 在 2020年12月3日 13:51 发表

219.239.98.* 在 2009年6月15日 09:44 发表

这个名词是谁提出的？什么年代提出的？

本文第一句话就说明了哟！

回复评论

发表评论请文明上网，理性发言并遵守有关规定。

查看

工具箱▼

质量屋

出自 MBA智库百科(https://wiki.mbalib.com/)

目录

什么是质量屋

质量屋的组成

QFD的工程应用过程概述

质量屋的案例分析

案例一：打火机质量屋实例^[1]

案例二:基于质量屋矩阵的产品模块划分方法^[2]

参考文献

温馨提示

本条目相关课程

本条目由以下用户参与贡献

评论(共21条)

导航

意见反馈

w_ii =	∑	s_ij
	j

查看

工具箱▼

质量屋

出自 MBA智库百科(https://wiki.mbalib.com/)

目录

什么是质量屋

质量屋的组成

QFD的工程应用过程概述

质量屋的案例分析

案例一：打火机质量屋实例[1]

案例二:基于质量屋矩阵的产品模块划分方法[2]

参考文献

温馨提示

本条目相关文档

本条目相关课程

本条目由以下用户参与贡献

评论(共21条)

导航

意见反馈

案例一：打火机质量屋实例^[1]

案例二:基于质量屋矩阵的产品模块划分方法^[2]