增长会计法
出自 MBA智库百科(https://wiki.mbalib.com/)
增长会计法(growth accounting approach)
目录 |
增长会计法(growth accounting approach) 的基本思路是以新古典增长理论为基础,将经济增长中要素投入贡献剔除掉,从而得到全要素生产率增长的估算值,其本质是一种指数方法。按照指数的不同构造方式,可分为代数指数法和几何指数法(也称索洛残差法) 。
1. 代数指数法(AIN)
代数指数法(arithmetic index number approach,AIN) 最早由艾布拉姆威兹(Abramvitz ,1956) 提出,其基本思想是把全要素生产率表示为产出数量指数与所有投入要素加权指数的比率。
假设商品价格为Pt ,数量为Qt ,则总产出为PtQt 。生产中资本投入为Kt ,劳动投入为Lt ,资本价格即利率为rt ,工资率为wt ,则总成本为rtKt + wtLt。在完全竞争和规模收益不变假设下,有总产出等于总成本即:
PtQt = rtKt + wtLt (1)
但由于技术进步等因素的影响, (1) 式往往不成立,可将(1) 式改写为:
P0Qt = TFPt[r0Kt + w0Lt] (2)
其中, r0 、w0 和P0 为基年利率、工资和价格。参数TFPt 为全要素生产率,反映技术进步等因素对产出的影响。由(2) 式可得:
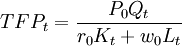 (3)
(3)
(3) 式就是全要素生产率的代数指数公式。后来,经济学家们又提出各种全要素生产率代数指数,它们的形式虽不同,但基本思想是一样的。
代数指数法很直观地体现出全要素生产率的内涵,但缺陷也十分明显,主要体现在它虽然没有明确设定生产函数,但暗含着资本和劳动力之间完全可替代,且边际生产率是恒定的,这显然缺乏合理性。所以这种方法更多地是一种概念化方法,并不适于具体实证分析(Caves ,Christensen andDiewart ,1982) 。
2. 索洛残差法(SR)
索洛残差法最早由罗伯特·索洛(Robert M. Solow,1957) 提出,基本思路是估算出总量生产函数后,采用产出增长率扣除各投入要素增长率后的残差来测算全要素生产率增长,故也称生产函数法。在规模收益不变和希克斯中性技术假设下,全要素生产率增长就等于技术进步率。 总量生产函数为:
Yt = Ω(t)F(Xt) (4)
其中,Yt为产出, 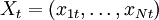 为要素投入向量, xnt为第n 种投入要素。假设Ω(t) 为希克斯中性技术系数,意味着技术进步不影响投入要素之间的边际替代率。进一步,假设F(·)为一次齐次函数即关于所有投入要素都是规模收益不变的。(4) 式两边同时对时间t 求导,并同除以(4) 式有:
为要素投入向量, xnt为第n 种投入要素。假设Ω(t) 为希克斯中性技术系数,意味着技术进步不影响投入要素之间的边际替代率。进一步,假设F(·)为一次齐次函数即关于所有投入要素都是规模收益不变的。(4) 式两边同时对时间t 求导,并同除以(4) 式有:
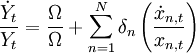 (5)
(5)
其中,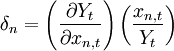 为各投入要素的产出份额。由(5) 式有:
为各投入要素的产出份额。由(5) 式有:
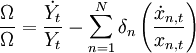 (6)
(6)
(6) 式就是全要素生产率增长的索洛残差公式,本质上是一个几何指数。各投入要素的产出份额δn 往往需要通过估算总量生产函数加以测算。具体估算中,常采用两要素(资本和劳动力) 的C - D 生产函数: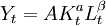 ,其中Yt 为现实产出,Lt 为劳动投入, Kt 为资本存量,α、β分别为平均资本产出份额和平均劳动力产出份额。两边同时取自然对数有:
,其中Yt 为现实产出,Lt 为劳动投入, Kt 为资本存量,α、β分别为平均资本产出份额和平均劳动力产出份额。两边同时取自然对数有:
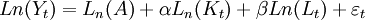 (7)
(7)
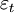 为误差项,通常我们假设α+β= 1 ,即规模收益不变,则有回归方程:
为误差项,通常我们假设α+β= 1 ,即规模收益不变,则有回归方程:
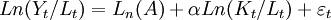 (8)
(8)
这是一个双对数模型,可以利用OLS 估算。其中资本存量需要测算,测算公式为:
Kt = It / Pt + (1 − δt)Kt − 1 (9)
其中Kt 为t 年的实际资本存量,Kt − 1 为t - 1 年的实际资本存量, Pt 为固定资产投资价格指数, It 为t 年的名义投资,δt 为t 年的固定资产的折旧率。在确定了资本存量的初值以及实际净投资后,便可以利用(7) 式给出各年的实际资本存量。这样,利用回归方程(8) ,我们可以估计出平均资本产出份额α和平均劳动力产出份额β,带入(6) 式可以得到全要素生产率增长率。索洛残差法开创了经济增长源泉分析的先河,是新古典增长理论的一个重要贡献(Lucas ,1988) 。但它也存在着一些明显缺陷:索洛残差法建立在新古典假设即完全竞争、规模收益不变和希克斯中性技术基础上,这些约束条件很强,往往难以满足;具体估算中,由于资本价格难以准确确定,所以利用资本存量来代替资本服务,忽略了新旧资本设备生产效率的差异以及能力实现的影响。此外,索洛残差法用所谓的“残差”来度量全要素生产率,从而无法剔除掉测算误差的影响。上述这些因素都不可避免地导致全要素生产率的估算偏差。[1]







