CGE模型
出自 MBA智库百科(https://wiki.mbalib.com/)
目录 |
可计算的一般均衡(Computable General Equilibrium,CGE)模型作为政策分析的有力工具,经过30多年的发展,已在世界上得到了广泛的应用,并逐渐发展成为应用经济学的一个分支。
世界上第一个CGE模型应是约翰森(Johansen)1960年提出的。在此之后,CGE模型的发展似乎出现了一段时间的中断,直到70年代都没有显著进步。在70年代,有两个因素引起了人们对CGE模型的兴趣。
1、世界经济面对着诸如能源价格或国际货币系统的突变、实际工资率的迅速提高等较大的冲击。
2、促使近20年来CGE模型的应用不断扩大的因素是其细化处理的能力日益提高。
为了真正理解CGE模型的含义,有必要简单回顾一下CGE模型的历史演变。CGE模型脱胎于利昂·瓦尔拉斯(L. Walras)的一般均衡理论。1874年,瓦尔拉斯提出了一般均衡的理论模型,用抽象的数学语言表述了一般均衡的思想。1936年,列昂节夫首次引入投入-产出模型,并假定成本是线性的、技术系数是固定的。不过,这些理论一般均衡模型的解的存在性至此还一直没有解决;理论一般均衡模型解的存在性、唯一性、优化性和稳定性直到50年代才由肯尼斯·约瑟夫·阿罗(Arrow)和罗拉尔·德布鲁(Gerard Debreu)给予证明。
尽管理论一般均衡模型的研究取得了如此的进步,但是,要将其应用于实际问题,还需解决相应模型解的算法问题。幸运的是,约翰森(Johansen,1960)构建了一个包括20个成本最小化的产业部门和一个效用最大化的家庭部门的实际一般均衡模型,并给出了相应的均衡价格的具体算法。由于约翰森模型的可计算性质,人们普遍把约翰森模型看作第一个CGE模型。1967年,斯卡夫(Scarf)研制了一种开创性的算法,用于对数字设定的一般均衡模型进行求解。斯卡夫关于均衡价格开创性的算法使得一般均衡模型从纯理论结构转化为可计算的实际应用模型成为可能,并大大地促进了大型实际CGE模型的开发和应用。
CGE模型是什么? 没有确切的定义;不过,可以给出一般性的描述。从本质上讲,CGE模型是多部门应用模型,设定在所有竞争性市场中不存在对商品和要素的超额需求或超额供给。这一描述有三点内容,反映了CGE模型的主要特征。
第一,CGE模型按照惯常的新古典微观经济理论方式明确设定所有经济主体的行为都是优化的,因而是关于一般而非局部经济主体行为的模型。
典型的CGE模型设定所有主体都是价格接受者,生产者在技术约束下追求成本最小化并获得零纯利润,消费者在预算约束下追求效用最大化。所有主体的需求和供给都来自这些最优化问题的解。通过使用这样的最优化行为假设,CGE模型强调了商品和要素的价格在影响主体的需求和供给决策中的作用。除生产者和居民外,模型还可以进一步包括政府、工会、资本创造者、进口和出口商等主体。
第二,它使用了市场均衡而非市场不均衡的假设,所有市场同时得到结清。
换言之,CGE模型刻划了不同经济主体的供给和需求决策对一些商品和要素价格的作用机制。在一般均衡条件下,所有商品和要素的数量和价格都同时内生决定。因此,CGE模型按一致方式考虑了整个经济的相互作用。
第三,它是可计算的而非纯理论性的,会生成具体的数字结果。
CGE模型使用数据描述某基准年度的经济,通过变更某组成要素而冲击经济并改变模型中所有数据项的值。CGE模型的核心数据是投入-产出帐户,CGE模型的基准实际上是某观察年度经济数据解的复制。CGE模型可以受到来自政策变动的冲击;通过求解 CGE模型可以得到冲击后的新的一般均衡状态。正是由于经济主体的行为方程因替代可能而被设定为高度非线性,CGE模型的数值解法才变得很复杂,很久之后才变得可计算并用于政策分析。
它所分析的基本经济单元是生产者、消费者、政府和外国经济。
1.生产行为
在CGE中,生产者力求在生产条件和资源约束之下实现其利润优化。这是一种次优解(Sub-optimal)。与生产者相关的有两类方程:一类是描述性方程,例如生产者的生产过程、中间生产过程等;另一类是优化条件方程。在许多CGE模型中,假设生产者行为可以用柯布—道格拉斯函数或常替代弹性(CES)方程来描述。
2.消费行为
也包括了描述性方程和优化方程。消费者优化问题的实质是在预算约束条件下选择商品(包括服务、投资以及休闲)的最夹组合以实现尽可能高的效益。
3.政府行为
一般来说,政府的作用首先是制定有关政策。在CEG中通常将这作为政府变量。同时,政府也是消费者。政府的收入来自税和费。政府开支包括各项公共事业、转移支付与政策性补贴。
4.外贸
在CGE中,通常按照常弹性转换方程(CET)来描述为了优化出口产品利润,把国内产品在国内市场和出口之间进行优化分配的过程。或用阿明顿(Armington)方程来描述为了实现最低成本把进口产品与国内产品进行优化组合的过程。
5.市场均衡
CGE的市场均衡及预算均衡包括如下几方面:
1)产品市场均衡。产品均衡不仅要求在数量上,而且要求在价值上。
2)要素市场均衡,主要是劳动力市场均衡,假定劳动力无条件迁移,不存在迁移的制 度障碍。
4)政府预算均衡。政府收入-政府开支=预算赤字。
5)居民收支平衡。居民收入的来源是工资及存款利息。居民收支平衡意味着:居民收入-支出=节余
6)国际市场均衡。外贸出超CGE中表现为外国资本流入,外贸入超表现为本国资本流出。
CGE模型经常被用来分析税收、公共消费变动,关税和其他外贸政策,技术变动,环境政策,工资调整,探明新的矿产资源储量和开采能力的变动等对国家或地区(国内或跨国的)福利、产业结构、劳动市场、环境状况、收入分配的影响。
CGE模型最重要的成功在于它在经济的各个组成部分之间建立起了数量联系,使我们能够考察来自经济某一部分的扰动对经济另一部分的影响。对于投入产出模型来讲,它所强调的是产业的投入产出联系或关联效应。而CGE模型则在整个经济约束范围内把各经济部门和产业联系起来,从而超越了投入产出模型。这些约束包括:对于政府预算赤字规模的约束,对于贸易逆差的约束,对于劳动、资本和土地的约束,以及处于环境考虑(如空气和水的质量)的约束等。
1.在分析政策变动对福利影响方面也仅获得了部分成功,因为它假定了政策变化不影响劳动力的非7失业和资本的水平、企业间竞争的形式和技术进步率。
2.CGE模型本身并不能提供有价值的预测工具
3.CGE模型需要的数据甚至比投入产出分析要远为复杂而难以找到,因为它不仅分析产业或工业,也分析个人,政府决策,这些都是投入产出分析力所不能及的。
为了使CGE模型有解,CGE模型必须封闭。这时,就要在各个目标之间进行折中,根据不同的取舍,分别称为凯恩斯式CGE模型、新古典CGE模型、金汉森CGE模型和科多润CGE模型(Koldorian)。
可计算非线性动态投入产出模型考虑把投入产出分析与CGE结合起来。
生产函数为: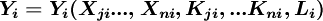
其中Xji为第i部门中间投入的第j部门产品的数量;Kji为第i部门所投入的第j部门固定资本产品的数量;Li为劳动工时投入量。
固定资本形成方程: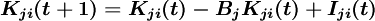
其中Kji为第i部门投入第j部门固定资本产品的数量。生产函数形式多样:
第一层的生产函数为: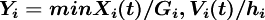
第二层的Xi为列昂剔夫型生产函数,而Vi则为CES型生产函数。
第三层的Ki为CES型生产函数。
![\boldsymbol{Y=A(p_1,...,p_n,r,w)Y+B(p_1,...,p_n,r,w)[Y(t+1)-Y(t)]+C(t)}](/w/images/math/0/a/2/0a2418451ad68cb704216d9e461809f7.png)
其中中间投入系数矩阵A(·,……,·)与固定资产使用系数矩阵B(· ,…,·)是价格,租金与工资率的函数。
可计算非线性动态投入产出模型有如下优点:
1.统计了列昂剔夫线性动态投入产出模型以及非线性静态与动态CGE模型。
2.参数估计更加可靠
3.采用叠代法计算速度快。
但其仍然未摆脱投入产出模型与CGE模型分析本身固有的一些缺陷。








不错啊!