探索性因子分析法
出自 MBA智库百科(https://wiki.mbalib.com/)
探索性因子分析法(Exploratory Factor Analysis,EFA)
目录 |
探索性因子分析法(Exploratory Factor Analysis,EFA)是一项用来找出多元观测变量的本质结构、并进行处理降维的技术。 因而,EFA能够将将具有错综复杂关系的变量综合为少数几个核心因子。
因子分析法是两种分析形式的统一体, 即验证性分析和纯粹的探索性分析。 英国的心理学家Charles Spearman在1904年的时候,提出单一化的智能因子(A Single Intellectual Factor)。 随着试验的深入,大量个体样本被分析研究,Spearman的单一智能因子理论被证明是不充分的。 同时,人们认识到有必要考虑多元因子。 20世纪30年代,瑞典心理学家Thurstone打破了流行的单因理论假设,大胆提出了多元因子分析(Multiple Factor Analysis)理论。 Thurstone在他的《心智向量》(Vectors of Mind, 1935)一书中,阐述了多元因子分析理论的数学和逻辑基础。
探索性因子分析和验证性因子分析的异同[1]
探索性因子分析和验证性因子分析相同之处
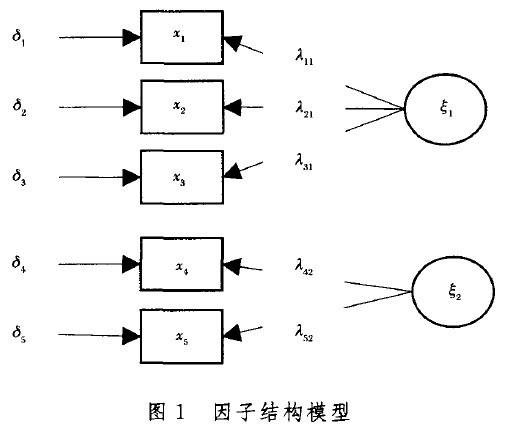
两种因子分析都是以普通因子分析模型作为理论基础,其主要目的都是浓缩数据,通过对诸多变量的相关性研究,可以用假想的少数几个变量(因子、潜变量)来表示原来变量(观测变量)的主要信息。图1所示即为最简单、也最为常见的因子模型,每个观测变量(指标)只在一个因子(潜变量)上负荷不为零,x1、x2 、x3是潜变量ξ1的指标,x4、x5是潜变量ξ2的指标。
将图1所示的因子模型推广至一般意义上的因子模型后,各观测变量x_i与m个公共因子ξ1,ξ2,...,ξm之间的关系可以用数学模型表示如下:
x1 = λ11ξ1 + λ12ξ2 + ... + λ1mξm + δ1
......
xk = λk1ξ1 + λk2ξ2 + ... + λkmξm + δk
其中:xi为各观测变量;ξi是公共因子;δi是xi,的特殊因子,有时也称误差项,包括xi的唯一性因子和误差因子两部分;λij是公共因子的负载;m是公共因子ξ1,ξ2,...,ξm的个数,k是各观测变量x1,...,xk的个数,m<k。上式也可以简单地用矩阵表示如下:x = Λxξ + δ
其中:
x = (x1,x2,...,xk)T , ξ = (ξ1,ξ2,...,ξm)T ,δ = (δ1,δ2,...,δk)T
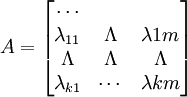 ,是负载矩阵
,是负载矩阵
探索性因子分析和验证性因子分析的差异之处
- 1.基本思想不同
因子分析的基本思想是要寻找公共因子,以达到降维的目的。探索性因子分析主要是为了找出影响观测变量的因子个数,以及各个因子和各个观测变量之间的相关程度,以试图揭示一套相对比较大的变量的内在结构。研究者的假定是每个指标变量都与某个因子匹配,而且只能通过因子载荷凭知觉推断数据的因子结构。而验证性因子分析的主要目的是决定事前定义因子的模型拟合实际数据的能力,以试图检验观测变量的因子个数和因子载荷是否与基于预先建立的理论的预期一致。指标变量是基于先验理论选出的,而因子分析是用来看它们是否如预期的一样。其先验假设是每个因子都与一个具体的指示变量子集对应,并且至少要求预先假设模型中因子的数目,但有时也预期哪些变量依赖哪个因子。
- 2.应用前提不同
探索性因子分析没有先验信息,而验证性因子分析有先验信息。探索性因子分析是在事先不知道影响因子的基础上,完全依据样本数据,利用统计软件以一定的原则进行因子分析,最后得出因子的过程。
在进行探索性因子分析之前,不必知道要用几个因子,以及各因子和观测变量之间的关系。在进行探索性因子分析时,由于没有先验理论,只能通过因子载荷凭知觉推断数据的因子结构。上述数学模型中的公共因子数m 在分析前并未确定,而是在分析过程中视中间结果而决定,各个公共因子ξi统一地规定为均影响每个观测变量xi。在管理研究中,如仅仅从数据出发,很难得到科学的结果,甚至可能与已有的理论或经验相悖。因此,探索性因子分析更适合于在没有理论支持的情况下对数据的试探性分析。这就需要用验证性因子分析来做进一步检验。而验证性因子分析则是基于预先建立的理论,要求事先假设因子结构,其先验假设是每个因子都与一个具体的指示变量子集对应,以检验这种结构是否与观测数据一致。也就是在上述数学模型中,首先要根据先验信息判定公共因子数m,同时还要根据实际情况将模型中某些参数设定为某一定值。这样,验证性因子分析也就充分利用了先验信息,在已知因子的情况下检验所搜集的数据资料是否按事先预定的结构方式产生作用。
- 3.理论假设不同
探索性因子分析的假设主要包括:①所有的公共因子都相关(或都不相关);②所有的公共因子都直接影响所有的观测变量;③ 特殊(唯一性)因子之间相互独立;④ 所有观测变量只受一个特殊(唯一性)因子的影响;⑤ 公共因子与特殊因子(唯一性)相互独立。验证性因子分析克服了探索性因子分析假设条件约束太强的缺陷,其假设主要包括:① 公共因子之间可以相关,也可以无关;② 观测变量可以只受一个或几个公共因子的影响,而不必受所有公共因子的影响;③特殊因子之间可以相关,还可以出现不存在误差因素的观测变量;④ 公共因子与特殊因子之间相互独立。
- 4.分析步骤不同
探索性因子分析主要有以下七个步骤:① 收集观测变量:通常采用抽样的方法,按照实际情况收集观测变量数据。② 构造相关矩阵:根据相关矩阵可以确定是否适合进行因子分析。③确定因子个数:可根据实际情况事先假定因子个数,也可以按照特征根大于1的准则或碎石准则来确定因子个数。④ 提取因子:可以根据需要选择合适的因子提取方法,如主成分方法、加权最小平方法、极大似然法等。⑤ 因子旋转:由于初始因子综合性太强,难以找出实际意义,因此一般都需要对因子进行旋转(常用的旋转方法有正交旋转、斜交旋转等),以便于对因子结构进行合理解释。⑥解释因子结构:可以根据实际情况及负载大小对因子进行具体解释。⑦计算因子得分:可以利用公共因子来做进一步的研究,如聚类分析、评价等。
而验证性因子分析主要有以下六个步骤:① 定义因子模型:包括选择因子个数和定义因子载荷。因子载荷可以事先定为0、或者其它自由变化的常数,或者在一定的约束条件下变化的数(比如与另一载荷相等)。② 收集观测值:根据研究目的收集观测值。③获得相关系数矩阵:根据原始资料数据获得变量协方差阵。④ 拟合模型:这里需要选择一种方法(如极大似然估计、渐进分布自由估计等)来估计自由变化的因子载荷。⑤ 评价模型:当因子模型能够拟合数据时,因子载荷的选择要使模型暗含的相关矩阵与实际观测矩阵之间的差异最小。常用的统计参数有:卡方拟合指数(x2)、比较拟合指数(CFI)、拟合优度指数(GFI)和估计误差均方根(RMSEA)。根据Bentler(1990)的建议标准,x2/DF≤3.0、CFI≥0.90、GFI≥0.85、RMSE≤0.05,则表明该模型的拟合程度是可接受的。⑥修正模型:如果模型拟合效果不佳,应根据理论分析修正或重新限定约束关系,对模型进行修正,以得到最优模型。
- 5.主要应用范围不同
探索性因子分析主要应用于三个方面:①寻求基本结构,解决多元统计分析中的变量间强相关问题;② 数据化简;③发展测量量表。验证性因子分析允许研究者将观察变量依据理论或先前假设构成测量模式,然后评价此因子结构和该理论界定的样本资料间符合的程度。因此,主要应用于以下三个方面:① 验证量表的维度或面向性(dimensionality),或者称因子结构,决定最有效因子结构;② 验证因子的阶层关系;③ 评估量表的信度和效度。
- 6.探索性因子分析和验证性因子分析的正确用法
从上述分析可以看出,探索性因子分析和验证性 因子分析是因子分析的两个不可分割的重要组成部分,在管理研究的实际应用中,两者不能截然分开,只有结合运用,才能相得益彰,使研究更有深度。An-derson,J.C.,Gerbin,D.W 建议,在发展理论的过程中,首先应通过探索性因子分析建立模型,再用验证提供了发析现模型以验证和修正的概念和计算工具,其提供的结果为验证性因子分析建立假设提供了重要的基础和保证。两种因子分析缺少任何一个,因子分析都将是不完整的 。一般来说,如果研究者没有坚实的理论基础支撑,有关观测变量内部结构一般先用探索性因子分析,产生一个关于内部结构的理论,再在此基础上用验证性因子分析,这样的做法是比较科学的,但这必须要用两组分开的数据来做。如果研究者直接把探索性因子分析的结果放到统一数据的验证性因子分析中,研究者就仅仅是拟合数据,而不是检验理论结构。如果样本容量足够大的话,可以将数据样本随机分成两半,合理的做法就是先用一半数据做探索性因子分析,然后把分析取得的因子用在剩下的一半数据中做验证性因子分析。如果验证性因子分析的拟合效果非常差,那么还必须用探索性因子分析来找出数据与模型之间的不一致。
在运用EFA法的时候,可以借助统计软件(如SPSS统计软件或SAS统计软件)来进行数据分析。
1、顾客满意度调查。
2、服务质量调查。
3、个性测试。
4、形象调查。
5、市场划分识别。
一个典型的EFA流程如下:
1、辨认、收集观测变量。
2、获得协方差矩阵(或Bravais-Pearson的相似系数矩阵)
3、验证将用于EFA的协方差矩阵(显著性水平、反协方差矩阵、Bartlett球型测验、反图像协方差矩阵、KMO测度)。
5、发现因素和因素装货。 因素装货是相关系数在可变物(列在表里)和因素(专栏之间在表里)。
6、确定提取因子的个数(以Kaiser准则和Scree测试作为提取因子数目的准则)。
7、解释提取的因子(例如,在上述例子中即解释为“潜在因子”和“流程因子”)。
1、EFA法便于操作。
2、当调查问卷含有很多问题时,EFA法显得非常有用。
3、EFA法既是其他因子分析工具的基础(如计算因子得分的回归分析),也方便与其他工具结合使用(如验证性因子分析法)。
1、变量必须有区间尺度。
2、沉降数值至少要要变量总量的3倍。
对于主因子分析法来说,不存在异常值、等距值、线形值、多变量常态分配以及正交性等情况。
EFA在教育、心理领域存在的问题及建议[2]
- 1.样本容量、观测变量数目不够
很多应用探索性因子分析的研究中,普遍存在的一个问题就是样本容量及观测变量数目太小。探索性因子分析中,一般要求样本容量至少为100-200,当变量的公共方差较大时,则一定数目的小样本也能确保因子负载的稳定性。国内学者曾做过一项调查,结果表明:1991-2000年国内两种心理学期刊发表的运用因子分析的文章中,有近10%的文章研究样本小于100,甚至有多达50%的文章没有提供这一信息。而对于观测变量的数目,一般认为,观测变量与所提取的因子数目之比至少为4。很多研究者认为观测变量的数目并不与被提取的因子数目相关联,因为研究者事先并不知道会有多少个因子被提取出来,因此,无法依据被提取的因子个数对观测变量的数目进行安排,但是,实际上很多研究者在因子分析前对所探讨的观测变量的因子结构已有了一定的预期。教育、心理领域中,存在着相当数量的研究并未达到这些标准。这或许是由于研究者对因子分析的要旨理解不深,但更有可能的是研究者对这类方法的细节重视不够。
- 2.因子提取方法的误用
探索性因子分析中最常用的提取因子的方法主要有两种:主成分分析法和主轴因子法。决定选用何种方法时,一般有两点值得考虑:一是因子分析的目的;二是对变量方差的了解程度。如果因子分析的目的是用最少的因子最大程度解释原始数据的方差,则应用主成分分析法;若因子分析的主要目的是确定数据结构,则适合用主轴因子法。
实际上,虽然研究者大多认为主成分分析法和主轴因子法的结果差别不大,但是Widman提出,主轴因子法使用复相关系数的平方作为公共方差的初始估计值,通过不断重复,最后得到确定的公共方差的值,所以,这一过程比起主成分分析法,因子负载就更准确。因此,他建议研究者最好使用主轴因子法而不是主成分分析法。但实际研究中,研究者大量使用的是主成分分析法,导致这一结果的最直接可能就是SPSS软件的缺省设置即为主成分分析法。
- 3.因子数目的确定标准及因子旋转中存在的问题
心理领域中,研究者运用的确定因子数目的标准大多是Kaiser法,即特征值≥1.0的标准。SPSS中,缺省的提取因子方法就是Kaiser法,但实际这一标准仅仅适用于主成分分析法。Fabrigar等人提出,特征值≥1.0的标准通常会导致提取过多的因子。当因子提取过多时,因子的重要性就值得怀疑了。例如,假设有这样的案例,分别从5个变量和10个变量中提取因子,在5个变量的情况下,特征值为1.0的因子将解释变量总方差的20%(1/5,每个变量的方差估计为1,总方差即为5);相应地,在10个变量的情况下,同样特征值为1.0的因子只能解释总体方差的10%(1/10),显然,当从大量变量中提取因子时,使用这样的标准将导致所提取的因子只能解释总方差很小的一部分。而碎石检验准则的主观性太强,并且,在有些情况下,因子的特征值并没有临界点,因为因子特征值是以一种线性的方式逐渐下降的,所以这种情况是可能存在的,例如双重负荷现象,因此,这种方法并没有太强的使用价值。一般推荐使用Reise等人的平行分析方法来确定因子的数目。这种标准比起碎石检验标准来说,减少了研究者主观因素的影响,结果也更客观、真实、有效。
虽然正交旋转能容易地解释和表示因子分析的结果,但由于其规定因子间不相关,因此正交旋转的结果往往并不符合实际。建议在探索性因子分析中使用斜交旋转法,它既能很容易地解释因子,同时也确保了因子间的简单结构,更重要的是,允许因子间的相关也更符合现实。例如,在探索性因子分析中提取出了家庭受教育水平和家庭经济收入这两个因子,如果勉强进行正交旋转,忽视两因子间的相关,必然会对结果造成很大的影响,实际上这两个因子都属于家庭社会经济地位的范畴,具有很高的相关,因此,进行斜交旋转,允许两因子间的相关,这样得到的结果才更有说服力。实际研究中,研究者更多地还是采用了正交旋转的方法,1991-2000年国内两种心理学期刊发表的运用因子分析的文章中,高达60%的文章使用正交旋转,而斜交旋转只占到了6%。
- 4.因子值缺乏重复验证性
心理、教育领域中,研究者求解因子值时,绝大多数依赖的是SPSS,而该软件所提供的求解因子值的方法最后求得的因子值是以一种加权的方式获得的,这就使得这些因子值只适用于特定的样本,缺乏重复验证性。
为了克服这一缺陷,研究者建议使用一种简单的非加权的方法,该方法首先鉴别出在某一因子上有较高负载的变量,然后将这些负载的值相加,从而得到能反映该因子的一种特定的因子值。使用这种方法研究者将失去变量在因子上的负载信息,但是,这样得到的因子值与SPSS提供的各种权重的因子值具有较高相关,因此,使用这种简单的策略获得的因子值是很有意义的,它能克服缺乏重复验证的缺陷。
当然,因子值本身实质上还是一种观测变量,存在一定的随机误差,可以使用潜变量模型的方法来消除这些随机误差。
- 5.研究结果的呈现形式不规范
因子分析结果的呈现中,哪些信息需要研究者明确提供都有一定的规定,但教育、心理领域的应用中,很少有研究者能提供完整的信息。作为因子分析的基础,相关矩阵是最根本的,研究者必须提供,否则,研究结果就缺乏重复验证的可能;另外,旋转前后因子所解释的方差、因子负载矩阵等信息也必须提供。
- 6.过于依赖SPSS,缺乏主动性
近年来因子分析应用中存在的最大的问题就是研究者过于依赖SPSS软件,往往是电脑控制人脑,研究者丧失了主动性。前面所讨论的因子分析实际应用中存在的一些主要问题,很大一部分是由SPSS本身所导致的。研究者进行因子分析时,大多脱离自己的实际研究,盲目地采用SPSS的各种缺省设置,最后导致获得的研究结果缺乏可信性,不符合实际研究的需要。例如,在连续性或非连续性(如二分类)变量的因子分析中,研究者应选择适当的分析方法,不能无视观测变量的类型,做统一的处理。对于由连续变量和非连续变量所组成的混合变量,研究者建议使用Tobit模型;分类顺序变量则应该采用最大似然法(Maximum Likelihood)或加权最小二乘法(Weighted Least Squares)。为了克服这种依赖性,有些研究者提出了采用其它的一些统计方法,逼迫研究者在进行统计分析时进行更多的思考,如CEFA软件。
总之,实际研究中,研究者应根据各种情况,选用适合的统计策略,尽量克服各种可能存在的问题,避免人脑受电脑的控制;另外,研究者自身加强统计知识的学习对于因子分析的正确运用也显得至关重要。
评论(共13条)
为什么看不懂? 看不懂啦~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~··· 都不举个例子……
如果拿实际数据举个例子会更容易懂
希望有了解的网友,帮忙贡献哦~
值得学习,其中对SPSS默认设置的依赖现象说得比较好,确实不少研究者在用SPSS的时候,分不清楚各种算法的优劣,比如主成分和最大似然,所以既然分不清,就干脆用默认的了;有时候球形度检验没结果或者结果不理想,也不管了,反正SPSS也能分析出结果来。这些都可能导致研究结果不准确。
Very helpful! if there is English version, it would be even more helpful!
Very helpful! if there is English version, it would be even more helpful! 很有幫助,謝謝








对于初哥来说,又懂得了一些分析方法选择的技巧.