ARMA模型
出自 MBA智库百科(https://wiki.mbalib.com/)
ARMA模型(Auto-Regressive and Moving Average Model)
目錄 |
ARMA 模型(Auto-Regressive and Moving Average Model)是研究時間序列的重要方法,由自回歸模型(簡稱AR模型)與滑動平均模型(簡稱MA模型)為基礎“混合”構成。在市場研究中常用於長期追蹤資料的研究,如:Panel研究中,用於消費行為模式變遷研究;在零售研究中,用於具有季節變動特征的銷售量、市場規模的預測等。
ARMA模型三種基本形式[1]
1.自回歸模型(AR:Auto-regressive);
自回歸模型AR(p):如果時間序列yt滿足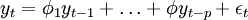
其中εt是獨立同分佈的隨機變數序列,且滿足:
E(εt) = 0 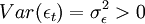
則稱時間序列為yt服從p階的自回歸模型。或者記為φ(B)yt = εt。
自回歸模型的平穩條件:
滯後運算元多項式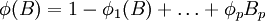 的根均在單位圓外,即φ(B) = 0的根大於1。
的根均在單位圓外,即φ(B) = 0的根大於1。
2.移動平均模型(MA:Moving-Average)
移動平均模型MA(q):如果時間序列yt滿足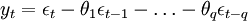
則稱時間序列為yt服從q階移動平均模型;
移動平均模型平穩條件:任何條件下都平穩。
3.混合模型(ARMA:Auto-regressive Moving-Average)
ARMA(p,q)模型:如果時間序列yt滿足: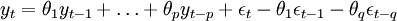
則稱時間序列為yt服從(p,q)階自回歸滑動平均混合模型。或者記為φ(B)yt = θ(B)εt
特殊情況:q=0,模型即為AR(p),p=0,模型即為MA(q),
將預測指標隨時間推移而形成的數據序列看作是一個隨機序列,這組隨機變數所具有的依存關係體現著原始數據在時間上的延續性。一方面,影響因素的影響,另一方面,又有自身變動規律,假定影響因素為x1,x2,…,xk,由回歸分析,
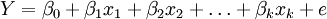
其中Y是預測對象的觀測值, e為誤差。作為預測對象Yt受到自身變化的影響,其規律可由下式體現,
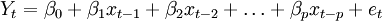
誤差項在不同時期具有依存關係,由下式表示,
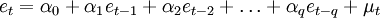
由此,獲得ARMA模型表達式:
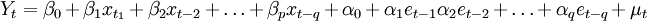
- ↑ 徐國祥,馬俊玲.《統計預測和決策》學習指導與習題[M].上海財經大學出版社.ISBN:7-81098-492-6.2005








在實際預測時,ut如何給出呢?