阿萊悖論
出自 MBA智库百科(https://wiki.mbalib.com/)
阿萊悖論(Allais Paradox)
目錄 |
阿萊(艾勒)悖論是決策論中的一個悖論。
1952年,法國經濟學家、諾貝爾經濟學獎獲得者阿萊作了一個著名的實驗:
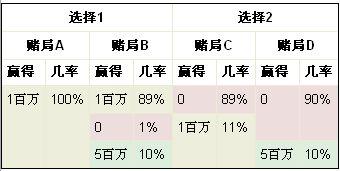
對100人測試所設計的賭局:
- 賭局A:100%的機會得到100萬元。
- 賭局B:10%的機會得到500萬元,89%的機會得到100萬元,1%的機會什麼也得不到。
實驗結果:絕大多數人選擇A而不是B。即賭局A的期望值(100萬元)雖然小於賭局B的期望值(139萬元),但是A的效用值大於B的效用值,
即1.00U(1m) > 0.89U(1m) + 0.01U(0) + 0.1U(5m)。【1】
然後阿萊使用新賭局對這些人繼續進行測試,
- 賭局C:11%的機會得到100萬元,89%的機會什麼也得不到。
- 賭局D:10%的機會得到500萬元,90%的機會什麼也得不到。
實驗結果:絕大多數人選擇D而非C。即賭局C的期望值(11萬元)小於賭局D的期望值(50萬元),而且C的效用值也小於D的效用值,
即0.89U(0) + 0.11U(1m) < 0.9U(0) + 0.1U(5m)。【2】
而由【2】式得 0.11U(1m) < 0.01U(0) + 0.1U(5m)
1.00U(1m) - 0.89U(1m) < 0.01U(0) + 0.1U(5m)
1.00U(1m) < 0.89U(1m) + 0.01U(0) + 0.1U(5m)
與【1】式矛盾,即阿萊悖論。
阿萊悖論的另一種表述是:按照期望效用理論,風險厭惡者應該選擇A和C;而風險喜好者應該選擇B和D。然而實驗中的大多數人選擇A和D。
阿萊悖論的解釋:出現阿萊悖論的原因是確定效應(Certain effect),即人在決策時,對結果確定的現象過度重視。
1、阿萊問題的提出
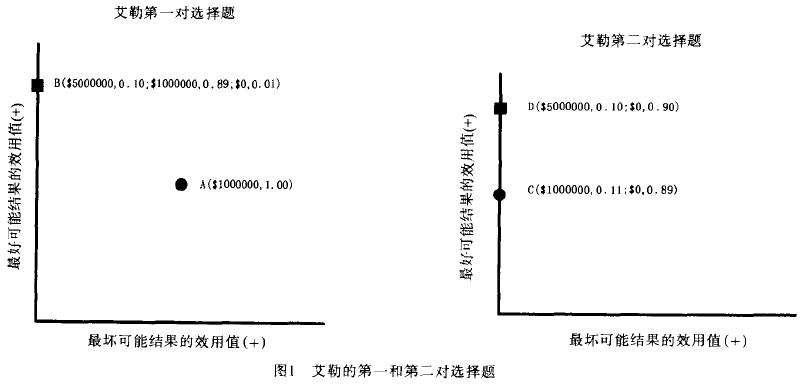
期望效用(Expected Utility)理論假設概率是線性的。針對其線性假設的最著名反例是阿萊悖論。阿萊悖論包含了兩對二擇一選擇題。阿萊所設計的原選擇問題與以下問題相近似:
從中可見,第一對選擇題包含一個肯定備擇方案和一個風險備擇方案。第二對選擇題實際上是從第一對選擇題脫胎而來:消除了一個各方案所共同擁有的可能結果(0.89的概率獲得$l 000 000),選擇A 便成了選擇C而選擇B便成了選擇D。據阿萊報告,面臨第一對二擇一選擇題時,大多數人偏愛A(肯定備擇方案),該選擇在期望效用理論里意味著:
u(1 000 000)>0.10u(5 000 000)+0.89u(1 000 000)+0.0lu(0)或(1-0.89)u(1 000 000)>0.10u(5 000 000)
然而,面臨第二對二擇一選擇題時,大多數人則偏愛D,該選擇在期望效用理論里意味著逆向的不等關係:
0.01u(1 000 000)<0.10u(5 000 000)
以上結果違背了期望效用理論的獨立性(independence)原則或稱為“確定事件原則”(surething principle)。依獨立性原則,人們對選擇 A(C)或選擇B(D)的偏愛不應受到由0.89的概率所產生的共同結果值($l 000 000或$0)的影響。
自阿萊悖論問世以來,研究者在70、80年代陸續積累了許多實驗證據,證明獨立性原則會被違背。決策領域也因此新發展了許多修訂線性假說的理性期望模型(rational expectations mode1)。這些模型大都從修正線性概率的假設人手,提出各可能結果的效用不再被客觀概率所乘,而是被非線性的決策權重(decision weights)所乘。而決策權重不必遵守概率的數學定律,並假定互補事件(complementary even)的決策權重之和可以小於1,即,w(P)+ w(1一P)< 1。從而將期望效用理論無法解釋為最大化反應的阿萊悖論等問題,又成功地描述為一種新的最大化的抉擇反應。
以極具代表性的Kahneman和Tversky的前景理論(prospect theory)為例,該理論提出了一個非線性的權重函數π。其中,大中概率被權重函數所低估(underweighted),小概率被權重函數所高估 (overweighted)。低估(underweighting)大中概率的結果可導致被權重的概率之和小於1,即,π(P)+ π(1-P)< 1。這種權重函數的特性被Kahneman 和Tversky稱之為“次確定性”(subcertainty)。正是這所謂的“次確定性 化解了阿萊所發現的悖論: (1-O.89) u(1,000,000)> 0.10u(5,000,000)>0.1lu(1,000,000),或,(1-0.89)>0.1l。請註意,期望理論是預先假定被人們選定的方案一定是具備了某種“最大值”的方案,即,在第一對選擇題中,A 的“總價值”>B的“總價值”;在第二對選擇題中,D 的“總價值”>C的“總價值”,從而演繹出“次確定性”關係:π(1.0)一π(0.89)>π(0.11)。
阿萊本人對阿萊悖論亦有自己的解釋。他在獲諾貝爾經濟學獎演講時,闡述了他對以他名字命名的阿萊悖論的看法:“阿萊悖論”只是在外表上顯得自相矛盾,它實際上蘊含了非常深刻的心理現實——接近確定事件時對安全的偏好。
該文對阿萊悖論所作的研究設計是基於對一所謂“齊當別”抉擇模型 的檢驗。這一抉擇模型認為決策者的認知能力無法勝任最優化模式所需要的精確定量計算,也不能夠以“效用”或者“心理距離”的方式表達對選擇對象整體估算的結果。因而假定:左右人類風險決策行為的機制不是最大限度地追求某種形式的期望(expectation)值,而是某種形式上辨察選擇對象之間是否存在優勢性(dominance)關係。藉助一表徵系統(最好和最壞可能結果維度)來描述涉及了阿萊選擇題的備擇方案,該模型將人類的抉擇行為描述為一種搜尋一備擇方案在主觀上優勢於另一備擇方案的過程。即:在方案A(C)在最壞可能結果維度上優越於方案B(D),而方案B(D)在最好可能結果維度上優越於方案A(c)的情況下,為了利用“弱優勢”(weak dominance)原則達成決策,人們必須在一維度上將差別較小的兩可能結果人為地“齊同”掉,而在另一維度上將“辨別”差別較大的兩可能結果作為最終抉擇的依據。
“齊當別”模型看阿萊悖論的方式與現代派生的理性期望模型很不一樣。該模型註意到,若假設人們對金錢的主觀價值函數(效用)為非線性的凹型,在第一對選擇題中,B方案的“壞結果”(獲零元)與 A方案的“肯定結果”(獲一百萬元)之間的差異顯得非常突出;而在第二對選擇題中,D方案的“好結果”(獲五百萬元)與C方案的“好結果 (獲一百萬元)之間的差異顯得非常突出(見圖1)。這意味著,在第一對選擇題中大部分人的決策是在最壞可能結果維度上進行,在第二對選擇題中大部分人的決策是在最好可能結果維度上進行。阿萊悖論的產生,是因為人們的先後兩次決策不是固定在同一維度上進行。
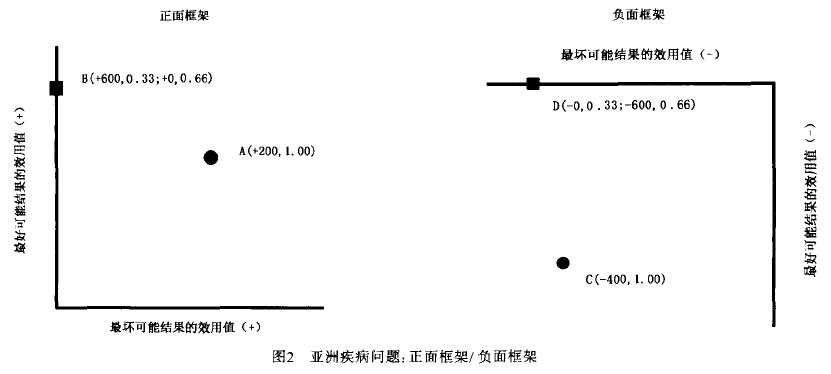
認為先後兩次決策不是在同一維度上進行,從而導致違背期望效用理論之公理的分析亦可應用於違背不變性(invariance)原則的“亞洲疾病問題。
在著名的“亞洲疾病問題 中,B方案的“零一結果 (最壞可能結果)與A方案的“肯定結果 (200人將生還)之間的差異在正面框架里顯得非常突出,而D 方案的“零一結果 (最好可能結果)與C方案的“肯定結果 (400人將死去)之間的差異在負面框架里顯得非常突出(見圖2)。這意味著,當正面表徵時大部分人的決策是在最壞可能結果維度上進行,當負面表徵時大部分人的決策是在最好可能結果維度上進行(操縱維度差別而產生的反例見Li )。
從圖1和圖2中可見,改變“共同結果值 和更替“正負框架 均可以改變最好和最壞可能結果維度上的相對差別。因此,如果研究者藉此嘗試將原問題中的維度差別朝相反方向轉換,便有可能產生與原阿萊悖論相反的選擇結果。在這種思路的指導下,作者設計了一系列涉及阿萊悖論的實驗,如,“登山隊問題州引以及“瓦斯爆炸問題 。在Li的登山隊問題中,被試所表現出的不一致的冒險趨勢也違背了期望效用理論的獨立性原則,但是其違背的類型與阿萊悖論完全相左。即大多數被試在第一對選擇題中選擇風險備擇方案,而在第二對選擇題中變換其選擇。這是因為,在第一對選擇題中,B方案的 “壞結果 (救活不了任何人)與A方案的“肯定結果 (肯定救活1人)之間的差異被設計成相對不顯著;而在第二對選擇題中,B方案的“壞結果 (89%的機會救活不了任何人)與A方案的“壞結果 (67%的機會救活不了任何人)之間的差異卻被設計成相對顯著。在Li和Adams的瓦斯爆炸問題中,期望效用理論的獨立性原則在正面框架中被人遵守但是在負面框架中卻被人違背。這是因為,在正框架里所操縱的“共同結果值”變化是為了促使大部分人的兩次決策都在最壞可能結果維度上進行,而在負框架里所操縱的“共同結果值 變化則是為了鼓勵大部分人的兩次決策分別在兩個不同可能結果維度上進行 (第一次決策是在次好 可能結果維度上進行;第二次決策是在最壞可能結果維度上進行)。所收集到的數據表明:只有“共同結果值 的變化能夠改變不同維度上可能結果的大小差異,阿萊悖論才有可能產生;改變了“共同結果值”而沒有改變不同維度上可能結果的大小差異,阿萊悖論則不可能產生。
為進一步驗證人們對阿萊選擇題的反應確實是受“齊當別 策略的支配,此項研究採用了一種稱為 “判斷 的任務。它將各備擇方案的最好結果相互配對,又將各備擇方案的最壞結果相互配對。然後要求被試判斷哪一種結果之間的差異最大。被試若判斷最好結果之間的差異最大,“齊當別”模式則推測,被試應挑選最好配對中擁有較好結果的方案(B或 D)。反之,被試若判斷最壞結果之間的差異最大, “齊當別 模式則推測,被試應避免最壞配對中擁有較壞結果的方案(B或D)。請註意,在第一對選擇題中,肯定方案的結果本身既可看成是最好結果(與 B的最好結果相比較時)又可看成是最壞結果(與B的最壞結果相比較時)。因此,人們選擇方案A(保守方案),是因為被試在最壞結果之間(“肯定獲一百萬元”對“0.01的概率獲得零元”)刻意避免了方案B 所提供的較壞結果(0.01的概率獲得零元);人們選擇方案B(冒險方案),是因為被試在最好結果之間 (“肯定獲一百萬元”對“0.10的概率獲得五百萬元 ) 精心挑選了方案B所提供的較好結果(0.10的概率獲得五百萬元)。
2、實驗
(1)實驗設計
1)材料
此項實驗要求被試次第完成兩種任務:選擇任務和判斷任務。選擇任務即阿萊的選擇題,呈現給被試的選擇題如前部所示。判斷任務如下所示:第一對判斷題(選出差別最大的配對)
- F:“肯定獲一百萬元”對“0.10的概率獲得五百萬元”
- G.“肯定獲一百萬元”對“0.01的概率獲得零元” 第二對判斷題(選出差另1最大的配對)
- I:“0.11的概率獲得一百萬元”對“0.10的概率獲得五百萬元”
- J:“0.89的概率獲得零元”對“0.90的概率獲得零元”
反應順序為:第一對選擇題、第一對判斷題、第二對選擇題、第二對判斷題。
2)實驗結果
阿萊式的選擇結果意味著,選擇類型與共同結果值之間存在著一定的關係。當共同結果的值為 $1,000,000時,人們喜歡肯定備擇方案;當共同結果的值減至$0時,人們變換其選擇方案。若考慮 “第三變數”(判斷類型),便可獲得更多的信息,並構成列聯表(表1)。
如表1所示,在第一次選擇和判斷中,此項實驗有過半數的被試(61%)喜歡風險方案B。其結果與阿萊式的選擇結果不盡相符,然而,選擇變異可以被判斷類型所解釋的效應(phi squared)為顯著性水平的11%(p<0.01)。另一方面,在第二次選擇和判斷中,此項實驗的大部分被試(92%)喜歡方案D。其結果非常符合阿萊式的選擇結果,其中亦有 7%(p<0.01)的選擇變異可以被判斷類型所解釋。
綜合兩次選擇和判斷的結果,一共有1 59次反應(65%)符合阿萊的立場。選擇類型與共同結果值之間存在顯著關係(x2(1):31.34,p<0.01)。另一方面,一共有182次反應(75%)符合“齊當別”抉擇模型的立場。共同結果值、判斷類型和選擇類型之間也存在著顯著關係(x2(3)= 52.47, p<0.01)。
3、討論
應用於風險狀態下決策的第一個規範性理論是期望值(Expected Value)理論 此後,迫於理論不能預測及解釋行為,人們不斷地對風險狀態下的決策模式進行修正。Bernoulli所討論的St.Petersburg悖論證明,如果人們的風險決策是某種期望值的最大化,這個期望值決不是EV。而阿萊悖論又證明,如果人們的風險決策還是某種期望值的最大化,這個期望值既不是EV也不是EU。然而,儘管在該領域的理論發展過程中涌現了許多自認為不同的決策模型,但當前的主流決策模型實際上只研究及採用了一種評價法則—— 期望法則(expectation rule)。證明期望法則具有合法性的理念一直驅動著這領域里的研究者。以後所派生出的理性期望模型 (rational expectations mode1)也只是朝著一個方向修正原有的舊模型。即預先假定被人們選定的方案一定是具備了某種“最大值”的方案,如果被選中的方案被證明不具備客觀上的“最大值”,那就轉而證明被選中的方案是具備了主觀上的“最大值”;如果通過對客觀風險結果或者對結果的客觀概率作適當地轉化後被選中的方案仍然被證明不具備某種 最大值”,那麼,就採用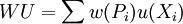 之類或者更複雜期望值的計算以證明被選中的方案具備了另一種“最大值”。理性期望模型的百年發展,從EU理論的傳統或Bemoullian版本 、到EU理論的yon Neumann和Morgenstem 版本、到Savage 的主觀 EU 理論 、到weighted utility模型 、到Rank-Dependent Utility、到sign-dependent utility模型、到rank-and sign-dependent utility模型等,均沒有跳出這個巢臼 。
之類或者更複雜期望值的計算以證明被選中的方案具備了另一種“最大值”。理性期望模型的百年發展,從EU理論的傳統或Bemoullian版本 、到EU理論的yon Neumann和Morgenstem 版本、到Savage 的主觀 EU 理論 、到weighted utility模型 、到Rank-Dependent Utility、到sign-dependent utility模型、到rank-and sign-dependent utility模型等,均沒有跳出這個巢臼 。
試借用一個決策小軼事來說明這領域里的研究者面臨悖論時的所作所為。這個軼事說的是如何測試一個小男孩(小時候的林肯總統?)的辨數能力。事由的起因是有人拿出兩枚硬幣,讓小男孩從中任挑一枚收下。結果,這小男孩選擇了一枚小面值的硬幣。消息傳開,眾人硬是不信。於是,接二連三有人用同樣的手法來重覆這種測驗。面對一枚小面值的硬幣和一枚大面值的硬幣之間作抉擇時,這小男孩總是毫不猶豫選擇了小面值的硬幣。
對小男孩這種屢試不爽的決策行為,經濟學家可能解讀為,該行為是違背了“最大化 原理的非理性行為。心理學家則可能會說,且慢,雖然被小男孩選中的硬幣被經濟學家證明不具備客觀意義的“最大值 ,但是,小男孩之所以選中該枚硬幣,是因為該枚硬幣對小男孩而言,是主觀上具備了“最大值 的硬幣:u(中選硬幣的值)>u(落選硬幣的值)。讓我們研究“金錢錯覺 ,特別是家境貧困孩子的“金錢錯覺 ,從而推導出這能使以上不等式成立的U函數。將客觀標準的值換成主觀標準的值後,小男孩的行為就變得可以理喻了。換言之,這領域里的研究者總是從預測失敗中想到“最大化 的標準可能出了差錯,要做的事是再接再厲修改不符實際的“最大化標準,而鮮有人懷疑“最大化 的原則本身會出錯。
然而,根據人們的實際選擇演繹出非線性的價值函數(如在受益和受損區域分別為凹型和凸型的 s狀價值函數v)和非線性的權重函數(如π函數),然後利用演繹出的非線性函數來讓人信服修正後的 “最大化 選擇模型是有效度的,這種做法並不能證明“最大化 假設本身是正確的。這樣做猶如能尋覓到證據來證明一古老的假設— — 地球是扁平的。尋求證據說明被選中的方案是可以被主觀函數演算成具有某種“最大值 ,就好比尋求證據說明心理反應 (如,扭曲,錯覺,放大等)是物理變化的非線性函數。雖然人們可以不斷找出比傳統對數函數更適合個體的心理物理函數,說該函數可使人們將地平線在主觀上知覺地更加“扁平 ,找到這樣的心理物理函數並不構成對“地球是扁平的 假設的證明。
此實驗收集到的數據表明,由判斷類型所揭示的“齊當別 策略能夠對不同“共同結果值 條件下的風險決策行為作出較連貫地解釋。這些結果連同 “登山隊問題 等結果,一道質疑了人類風險決策行為是某種期望值的最大化的說法。也許,不斷修正的期望模型最終又能演繹出新的主觀價值函數或主觀概率函數,將人們的風險決策行為圓滿地描述為最大化過程;也許,指導人們作風險決策的原則根本就不是期望法則,有如Simon的“滿意法則 (satisficing) ,須修正的期望模型只不過是為掩蓋舊錯誤而犯下的新錯誤,現在到了後來人考慮擺脫 “期望法則 隆圈的時候了。
回到小男孩的選擇問題,在最後一次測驗時他如是說:“如果我選了大面值的硬幣,你們還會一而再、再而三地試我嗎?
本条目由以下用户参与贡献
山林,沙漠之鹰,funwmy,Vulture,Wwdz,Angle Roh,Dan,Cabbage,Zfj3000,Lweij,Yixuanzhan,KAER,金龙,^_~,LuyinT,Tracy.評論(共13條)
從中可見,第一對選擇題包含一個肯定備擇方案和一個風險備擇方案。第二對選擇題實際上是從第一對選擇題脫胎而來:消除了一個各方案所共同擁有的可能結果(0.89的概率獲得$l 000 000),選擇A 便成了選擇C而選擇B便成了選擇D。
哪裡有共同擁有的可能結果??? 求解答。
文末對“決策依據是期望值最大化”進行了質疑,本來是很好的,可惜卻引用了小男孩的故事,故事末尾是小男孩希望在多次的博弈中獲得最多的貨幣。這樣一來質疑顯得無力。
thats why prospect theory shows that when people face losses, they will have risk seeking behavior










我感覺反正也是冒險,一百萬和五百萬,多冒1%的險就有四百萬的差距,誰也會選擇D啊~~~(個人感覺不涉及精密計算)