超模博弈
出自 MBA智库百科(https://wiki.mbalib.com/)
超模博弈(Supermodular Game)
目錄 |
超模博弈是博弈論中另一個重要的概念,在超模博弈中,每個參與者增加其策略所引起的邊際效用隨著對手策略的遞增而增加。博弈里最優反應的對應是遞增的,所以參與者的策略是“策略互補的”。當有兩個參與者時,對變數進行變化以後還可以用這個框架來分析遞減的最優反應的情形(即策略替代)。超模博弈的定義是:對於參與者vj#i∈N,都滿足:
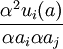 ≥0
≥0
超模博弈理論最早由Topkis(1978)創立,它建立在格子規劃的基礎之上,為分析具有互補策略的博弈提供了一個一般的方法。具有互補策略的博弈是指博弈中參與人的最優反應對應關於對手的策略遞增,從而參與人的策略體現出一定的互補性。由於超模博弈理論建立在格子理論的基礎之上,因而它不需要傳統最優化理論中的凸性及可微性假設,而只需要策略空間的一定的序結構及目標函數的一定的弱連續性和單調性。更重要的是這種博弈具有很好的性質,它具有純策略的Nash均衡,並且Nash均衡集也具有一定的序結構。超模博弈理論首先被Vives(1985,1990)及Milgrom和Roberts(1990)發展:Vives給出了超模博弈中Nash均衡的存在性及序結構;Milgrom等廣泛分析了超模博弈在經濟學中的具體應用,指出超模博弈中純策略的Nash均衡集,相關均衡集及可理性化均衡集具有相同的邊界,且這些邊界關於外生參數單調。Milgrom和Shannon(1994)將以前關於基數超模博弈的概念發展到序數超模博弈,並研究了序數超模博弈中的比較靜態分析(文中所提到的超模博弈如不特別指明都指基數超模博弈)。Athey(2001)運用超模博弈理論分別研究了不完全信息博弈及多期動態投資博弈中純策略均衡的特性]。Echenique(2003)研究了具有互補策略博弈的混合策略均衡及擴展式博弈中的均衡。Echenique(2004)一反以往的研究邏輯,探討了在允許按照某種規則對博弈的均衡進行排序的情況下博弈成為策略互補的條件。索洪敏(2006)研究了有序Banach空間上超模博弈的Nash均衡的存在性。
超模博弈理論[1]
一個集合S若對於其中任意兩個元素x和y,和y的上下確界都在S中,其中上確界記為x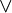 y,而下確界記x
y,而下確界記x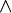 y,則稱S為格子。從格子S到實數R上的函數f,,即f:S
y,則稱S為格子。從格子S到實數R上的函數f,,即f:S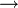 R,若對於
R,若對於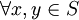 ,都有f(x)+f(y)≤f(x
,都有f(x)+f(y)≤f(x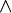 y)+f(x
y)+f(x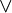 y),則稱,則稱f(x)為S上的超模函數。若logf(x)為超模的,則稱f(x)為對數超模的。超模函數在工程、經濟等方面都有著廣泛的應用。目標函數的超模性在經濟上代表著互補的投入。這裡我們所指的超模性是基數超模,因為函數的值域為實數R。與基數超模性相對應的有序數超模性,即擬超模。若S1為一個格子,而S2為一個偏序集,函數
y),則稱,則稱f(x)為S上的超模函數。若logf(x)為超模的,則稱f(x)為對數超模的。超模函數在工程、經濟等方面都有著廣泛的應用。目標函數的超模性在經濟上代表著互補的投入。這裡我們所指的超模性是基數超模,因為函數的值域為實數R。與基數超模性相對應的有序數超模性,即擬超模。若S1為一個格子,而S2為一個偏序集,函數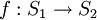 若滿足:對於S1中任意的x'及x,只要f(x'
若滿足:對於S1中任意的x'及x,只要f(x' 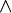 x)<f(x'),就有f(x)<f(x'
x)<f(x'),就有f(x)<f(x'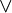 x),則稱函數f(x)為S1上的擬超模函數(文中所有的順序關係都為對應集合中的順序關係)。很顯然如果一個函數為超模的,則它必定為擬超模的。擬超模是超模概念的序數推廣,它只要求函數的值域為一般的偏序集,因而在經濟學中有著更廣泛的應用。
x),則稱函數f(x)為S1上的擬超模函數(文中所有的順序關係都為對應集合中的順序關係)。很顯然如果一個函數為超模的,則它必定為擬超模的。擬超模是超模概念的序數推廣,它只要求函數的值域為一般的偏序集,因而在經濟學中有著更廣泛的應用。
與變數之間的互補性相對應的另外一個重要概念是增差。S1與S2是兩個格子,函數f:S1×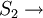 R若滿足,對S1中任意的x及x',其中x≥x',S2中任意的y,都有f(x,y)一f(x',y)關於y遞增,則稱函數f(x,y)在(x,y)具有增差。在一個博弈中,如果3x代表某一個參與人的策略,y代表另一個參與人的策略,而f(x,y)代表第一個參與人的支付函數,則f(x,y)在(x,y)具有增差意味著參與人之問策略的互補性,即當第二個參與人增加他的行動變數時,第一個參與人也會增加他的行動變數。
R若滿足,對S1中任意的x及x',其中x≥x',S2中任意的y,都有f(x,y)一f(x',y)關於y遞增,則稱函數f(x,y)在(x,y)具有增差。在一個博弈中,如果3x代表某一個參與人的策略,y代表另一個參與人的策略,而f(x,y)代表第一個參與人的支付函數,則f(x,y)在(x,y)具有增差意味著參與人之問策略的互補性,即當第二個參與人增加他的行動變數時,第一個參與人也會增加他的行動變數。
由於文中所討論的博弈的策略空間為連續的,所以規定實數R上的順序關係為通常的序關係,而對於維歐氏空間中的向量x=(x1,...,xn)與y=(y1,...,yn),x≥y等價於xi≥yi,其中i=1,...,n.。另外由於目標函數一般為光滑的,所以有些定理為原始定理的特殊情況。函數的超模與增差在經濟上都代表著互補性,如下的引理給出了它們之間的關係(引理的證明請參照相應的參考文獻)。
引理2.1:Rn上的函數f為超模的充要條件為f在Rn上具有增差(其中在多個變數上具有增差是指在任意兩個變數對上具有增差)。
對於歐氏空間中的光滑函數,關於函數的超模與增差有如下結論。
引理2.2:設I=[x,x]為Rn中的區間,若函數f: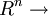 R在包含I的某個開區間上二次連續可微,則f在I上為超模函數的充要條件為,
R在包含I的某個開區間上二次連續可微,則f在I上為超模函數的充要條件為, i≠j,
i≠j,
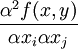 ≥0。
≥0。
由此可以看到對於常見的二次可微函數,超模性的要求非常簡單,它只要求交叉偏導非負,對於二階偏導沒有任何要求,也不需要函數的凹性。對應於歐氏空間中可微的支付函數,下麵給出光滑的超模博弈的概念。
博弈Γ={N,Sn,fn},其中Sn∈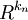 ,若滿足下麵四個條件
,若滿足下麵四個條件
1)Sn為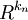 中的閉區間。
中的閉區間。
2)fn在Sn上二次連續可微。
3)f_n在S_n上超模,即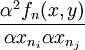 ≥0,其在i≠j,1≤i,j≤n。
≥0,其在i≠j,1≤i,j≤n。
4)fn在(Sn,Sm)上增差,即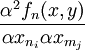 ≥0,其中m≠n,1≤i≤k,1≤≤k。
≥0,其中m≠n,1≤i≤k,1≤≤k。
則稱為光滑的超模博弈。
以下關於超模博弈中純策略Nash均衡的存在性及單調性定理為超模博弈理論的基礎。它不僅保證了超模博弈中純策略Nash均衡的存在性,還保證了極值均衡的存在性。
引理2.3:若Γ為一個超模博弈,則純策略的Nash均衡存在,且對於策略空間上給定的序結構,最大最小的純策略Nash均衡存在。
- ↑ 楊曉花,羅雲峰,吳輝球.Bertrand模型與超模博弈[J].中國管理科學,2009(1)







