二項分佈
出自 MBA智库百科(https://wiki.mbalib.com/)
二項分佈(Binomial distribution)
二項分佈是一種具有廣泛用途的離散型隨機變數的概率分佈,它是由貝努里始創的,所以又叫貝努里分佈。
二項分佈是指統計變數中只有性質不同的兩項群體的概率分佈。所謂兩項群體是按兩種不同性質劃分的統計變數,是二項試驗的結果。即各個變數都可歸為兩個不同性質中的一個,兩個觀測值是對立的。因而兩項分佈又可說是兩個對立事件的概率分佈。
目錄 |
二項分佈用符號b(x.n.p),表示在n次試驗中有x次成功,成功的概率為p。
二項分佈的概率函數可寫作:
b(x.n.p)=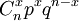
式中x=0、1、2、3.....n為正整數
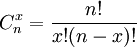
兩項分佈中含有兩個參數n與p,當它們的值已知時,便可計算出分佈列中各概率的值。
例1 擲硬幣試驗。有10個硬幣擲一次,或1個硬幣擲十次。問五次正面向上的概率是多少?
解:根據題意n=10,p=q=1/2,x=5
b(5、l0、1/2) = 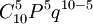
= 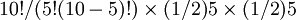
= 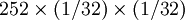
= 0.24609
所以五次正面向上的概率為0.24609
此題若問五次及五次以上正面向上的概率是多少?
解:此題要求出五次及五次以上正面向上的概率之和。正面有五次、六次、七次、八次、九次、十次。依公式5—10應為:
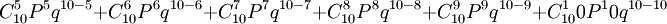
= 252/1024+210/1024+120/1024+45/1024+10/1024+1/1024
= 638/1024
= 0.623
五次及五次以上正面向上的概率為0.623
此題各項展開式的繫數,若用楊輝三角計算也十分方便。讀者:前面的楊輝三角寫到(p + q)10。試比較五次及五次以—LK面向;的各項繫數是否為252、210、120、45、10、1。
(一)二項分佈是離散型分佈,概率直方圖是躍階式的。因為x為不連續變數,用概率條圖表示更合適,用直方圖表示只是為了更形象些。
1.當p=q時圖形是對稱的
例2 (p + q)6,p=q=1/2,各項的概率可寫作:
p6 + 6p5q + 15p4q2 + 20p3q3 + 15p2q4 + 6plq5 + q6
= 1/64+6/64+15/64+20/64+15/64+6/64+1/64
= 1
2.當p≠q時,直方圖呈偏態,p<q與p>q的偏斜方向相反。如果n很大,即使p≠q,偏態逐漸降低,最終成正態分佈,二項分佈的極限分佈為正態分佈。故當n很大時,二項分佈的概率可用正態分佈的概率作為近似值。何謂n很大呢?一般規定:當p<q且np≥5,或p>q且nq≥5,這時的n就被認為很大,可以用正態分佈的概率作為近似值了。
如果二項分佈滿足p<q,np≥5,(或p>q,np≥5)時,二項分佈接近正態分佈。這時,也僅僅在這時,二項分佈的x變數(即成功的次數)具有如下性質:
μ = np (5—10a)
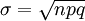 (5—10b)
(5—10b)
即x變數具有μ = np ,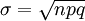 的正態分佈。
的正態分佈。
式中n為獨立試驗的次數,
p為成功事件的概率,q=1- p。 由於n很大時二項分佈逼近正態分佈,其平均數,標準差是根據理論推導而來的,故用μ和σ而不用X和S表示。它們的含意是指在二項試驗中,成功的次數的平均數μ = np ,成功次數的分散程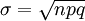 。例如一個擲10枚硬幣的試驗,出現正面向上的平均次數為5次(μ= np=
。例如一個擲10枚硬幣的試驗,出現正面向上的平均次數為5次(μ= np=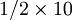 ),正面向上的散佈程度為10×(1/2)×(1/2)= 1.58(次),這是根據理論的計算,而在實際試驗中,有的人可得10個正面向上,有人得9個、8個……,人數越多,正面向上的平均數越接近5,分散程度越接近1.58。
),正面向上的散佈程度為10×(1/2)×(1/2)= 1.58(次),這是根據理論的計算,而在實際試驗中,有的人可得10個正面向上,有人得9個、8個……,人數越多,正面向上的平均數越接近5,分散程度越接近1.58。
1.各觀察單位只能具有相互對立的一種結果,如陽性或陰性,生存或死亡等,屬於兩分類資料。
2.已知發生某一結果(陽性)的概率為π,其對立結果的概率為1-π,實際工作中要求π是從大量觀察中獲得比較穩定的數值。
3.n次試驗在相同條件下進行,且各個觀察單位的觀察結果相互獨立,即每個觀察單位的觀察結果不會影響到其他觀察單位的結果。如要求疾病無傳染性、無家族性等。
項分佈在心理與教育研究中,主要用於解決含有機遇性質的問題。所謂機遇問題,即指在實驗或調查中,實驗結果可能是由 ?猜測而造成的。比如,選擇題目的回答,劃對劃錯,可能完全由猜測造成。凡此類問題,欲區分由猜測而造成的結果與真實的結果之間的界限,就要應用二項分佈來解決。
例3有正誤題10題,問答題者答對幾題才能認為他是真會,或者說答對幾題,才能認為不是出於猜測因素?
此題p=q=1/2,即猜對猜錯的概率各為0.5。np≥5,故此二項分佈接近正態分佈:
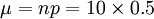 =5
=5
根據正態分佈概率,當Z=1.645時,該點以下包含了全體的95%。如果用原分數表示,則為
 =7.6≈8
=7.6≈8
它的意義是,完全憑猜測,10題中猜對8題以下的可能性為95%,猜對8、9、10題的概率只5%。因此可以推論說,答對8題以上者不是憑猜測,而是會答。但應該明確:作此結論,也仍然有犯錯誤的可能,即那些完全靠猜測的人也有5%的可能性答對8、9、10道題。
此題的概率值,還可用二項分佈函數直接計算,亦得與正態分佈近似的結果:
b(8 10 0.5)=C102p8q2 =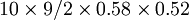 = 45/1024
= 45/1024
b(9 10 0.5)=C101p9q1 = = 10/1024
= 10/1024
b(10 10 0.5) =C100p10= 1/1024
根據概率加法,答對8題及其以上的總概率為:45/1024+10/1024+1/1024=56/1024 = 0.0547 同理,可計算8題以下的概率為 95%。(近似).
例4有10道多重選擇題,每題有5個答案,其中只有一個是正確的。問答對幾題才能說不是猜的結果?
此題n=10,p=1/5 = 0.2,q = 0.8,np<5,故此題不接近正態分佈,不能用正態分佈計算概率,而應直接用二項分佈函數計算猜時各題數的概率:
b(10、10、0.2)=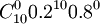 =
= =0.000000102
=0.000000102
b(9、10、0.2)=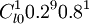 =
=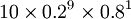 =0.000004096
=0.000004096
b(8、10、0.2)= 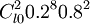 =
=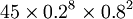 =0.000073728
=0.000073728
b(7、10、0.2)= =
=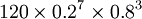 =0.000786432
=0.000786432
b(6、10、0.2)= =
=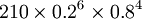 =0.00550524
=0.00550524
b(5、10、0.2)=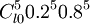 =
=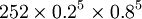 =0.026424115
=0.026424115
b(4、10、0.2)=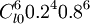 =
=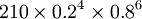 =0.088080384
=0.088080384
根據以上所計算的猜對各題數的概率,可用概率加法求得猜對5題及5題以上的概率為0.03279,不足5%,故可推論說答對5題以上者可算真會,作此結論仍有3.3%犯錯誤的可能。
若上例中題數增加到30題,則np>5,就可用正態分佈的概率計算:
解: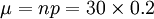 =6
=6
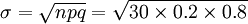 =2.191
=2.191
X=μ+1.645×σ=6 +1.645×2.191=9.6
因此可得結論,答對10題或10題以上,才能被認為是真會。作此結論犯錯誤的概率為5%。
如果想使推論犯錯誤的概率降為1%,則根據正態分佈可求得此時的z=2.33,使用相同的計算方法,只將2.33代替1.645,可求得臨界的分數(或答對的題數)。








超出了高中的水平,我唯有嘆息..