離散信源
出自 MBA智库百科(https://wiki.mbalib.com/)
- 離散信源(Discrete Information Source)
目錄 |
什麼是離散信源[1]
離散信源是指信源輸出符號為離散隨機變數的信源。
設離散信源輸出隨機變數X的值域R為一離散集合R={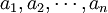
}，其中，n可以是有限正數，也可以是可數的無限大正數。若已知R上每一消息發生的概率分佈為
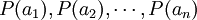
則離散信源X的概率空間為
![[R,P]=[X,P]=\begin{bmatrix} a_1 & a_2 & \cdots & a_n \\ P(a_1) & P(a_2) & \cdots & P(a_n) \end{bmatrix}](/w/images/math/f/c/5/fc5d9a82e42123bc2b39676e8cc6c0ea.png)
其中，信源輸出消息的概率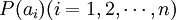
滿足：
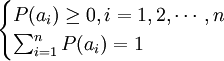
離散信源的信息量[2]
離散信源產生的消息狀態是可數的或者離散的，離散消息中所包含的信息的多少(即信息量)應該怎麼樣來衡量呢?
經驗告訴人們，當某個消息出現的可能性越小的時候，該消息所包含的信息量就越多。消息中所包含的信息的多少與消息出現的概率密切相關。
為此，哈特萊首先提出了信息的度量關係。
對於離散消息xi來講，其信息量I可表示為
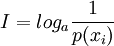
其中，p(xi)表示離散消息xi出現的概率。
根據a的取值不同，信息量的單位也不同。當a取2時，信息量的單位為比特(bit)；當a取e時，信息量的單位為奈特；當a取10時，信息量的單位為哈特萊。通常口的取值都是2，即用比特作為信息量的單位。
離散信源的熵[2]
當離散消息中包含的符號比較多時，利用符號出現概率來計算該消息中的信息量往往是比較麻煩的。為此，可以用平均信息量(H)來表徵，即
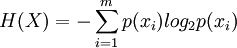
其中，m表示消息中的符號個數。
離散信源的分類[3]
根據輸出符號問的依賴關係，離散信源可以分為無記憶信源和有記憶信源，輸出符號間相互獨立的稱為無記憶信源，而輸出符號之間具有相關性的，稱為有記憶信源。最簡單的無記憶信源的例子就是擲骰子試驗，其中每次拋擲結果都獨立於其他拋擲結果。如果骰子是均勻的，那麼我們就認為每次拋擲出現某點數的概率是相等的，即等於1／6。有記憶信源的最典型的例子就是自然語言。例如，書寫的文章或講話中每一個詞或字、字母都和它前後的符號有關。最簡單的有記憶信源就是馬爾可夫信源，自然語言可以用馬爾可夫信源近似。
統計特性不隨時問起點改變的信源稱為平穩信源，反之稱為非平穩信源。
