离散信源
出自 MBA智库百科(https://wiki.mbalib.com/)
- 离散信源(Discrete Information Source)
目录 |
什么是离散信源[1]
离散信源是指信源输出符号为离散随机变量的信源。
设离散信源输出随机变量X的值域R为一离散集合R={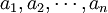
}，其中，n可以是有限正数，也可以是可数的无限大正数。若已知R上每一消息发生的概率分布为
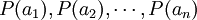
则离散信源X的概率空间为
![[R,P]=[X,P]=\begin{bmatrix} a_1 & a_2 & \cdots & a_n \\ P(a_1) & P(a_2) & \cdots & P(a_n) \end{bmatrix}](/w/images/math/f/c/5/fc5d9a82e42123bc2b39676e8cc6c0ea.png)
其中，信源输出消息的概率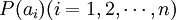
满足：
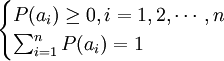
离散信源的信息量[2]
离散信源产生的消息状态是可数的或者离散的，离散消息中所包含的信息的多少(即信息量)应该怎么样来衡量呢?
经验告诉人们，当某个消息出现的可能性越小的时候，该消息所包含的信息量就越多。消息中所包含的信息的多少与消息出现的概率密切相关。
为此，哈特莱首先提出了信息的度量关系。
对于离散消息xi来讲，其信息量I可表示为
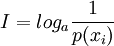
其中，p(xi)表示离散消息xi出现的概率。
根据a的取值不同，信息量的单位也不同。当a取2时，信息量的单位为比特(bit)；当a取e时，信息量的单位为奈特；当a取10时，信息量的单位为哈特莱。通常口的取值都是2，即用比特作为信息量的单位。
离散信源的熵[2]
当离散消息中包含的符号比较多时，利用符号出现概率来计算该消息中的信息量往往是比较麻烦的。为此，可以用平均信息量(H)来表征，即
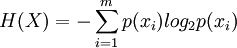
其中，m表示消息中的符号个数。
离散信源的分类[3]
根据输出符号问的依赖关系，离散信源可以分为无记忆信源和有记忆信源，输出符号间相互独立的称为无记忆信源，而输出符号之间具有相关性的，称为有记忆信源。最简单的无记忆信源的例子就是掷骰子试验，其中每次抛掷结果都独立于其他抛掷结果。如果骰子是均匀的，那么我们就认为每次抛掷出现某点数的概率是相等的，即等于1／6。有记忆信源的最典型的例子就是自然语言。例如，书写的文章或讲话中每一个词或字、字母都和它前后的符号有关。最简单的有记忆信源就是马尔可夫信源，自然语言可以用马尔可夫信源近似。
统计特性不随时问起点改变的信源称为平稳信源，反之称为非平稳信源。
