波爾查諾-魏爾斯特拉斯定理
出自 MBA智库百科(https://wiki.mbalib.com/)
目錄 |
波爾查諾-魏爾施特拉斯定理是指數學拓撲學與實分析中用以刻劃 中的緊集的基本定理,得名於數學家伯納德•波爾查諾與卡爾•魏爾施特拉斯。波爾查諾-魏爾斯特拉斯定理說明,有限維實數|實向量空間
中的緊集的基本定理,得名於數學家伯納德•波爾查諾與卡爾•魏爾施特拉斯。波爾查諾-魏爾斯特拉斯定理說明,有限維實數|實向量空間 中的一個子集E是緊集序列(每個序列都有收斂子序列)當且僅當E是有界閉集。
中的一個子集E是緊集序列(每個序列都有收斂子序列)當且僅當E是有界閉集。
這個定理最早由伯納德•波爾扎諾證明,當他在證明介值定理時,附帶證明瞭這個定理,但是他的證明已經散佚。卡爾•魏爾施特拉斯獨自發現並證明瞭這個定理。波爾扎諾-魏爾施特拉斯定理是實分析中的基本定理。
子列:也稱為子序列。一個序列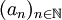 的一個子列是指在
的一個子列是指在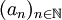 中抽取無窮多個元素,然後按照它們在原來序列里的順序排列起來的序列。嚴格的定義是:如果存在一個從
中抽取無窮多個元素,然後按照它們在原來序列里的順序排列起來的序列。嚴格的定義是:如果存在一個從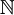 到
到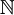 的嚴格單調遞增的映射φ,使得
的嚴格單調遞增的映射φ,使得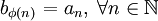 ,就稱
,就稱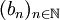 是
是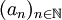 的一個子列。
的一個子列。
有界閉集: 中的有界閉集概念建立在給定的拓撲和度量上的。由於在有限維向量空間中所有度量等價,所以可以將
中的有界閉集概念建立在給定的拓撲和度量上的。由於在有限維向量空間中所有度量等價,所以可以將 視為裝備了歐幾里德度量的度量空間(並且可以定義相應的範數)。
視為裝備了歐幾里德度量的度量空間(並且可以定義相應的範數)。 的子集E有界,當且僅當所有E中元素x的範數小於一個給定常數K。註意這時對應的拓撲是歐幾里德範數誘導的自然拓撲。
的子集E有界,當且僅當所有E中元素x的範數小於一個給定常數K。註意這時對應的拓撲是歐幾里德範數誘導的自然拓撲。
序列緊致:稱一個集合S是序列緊致的,是指每個由集合S中元素所組成的數列都包含極限(序列)|收斂的子列,並且該子列收斂到集合S中的某個元素。
波爾查諾-魏爾斯特拉斯定理可以視為刻畫有限維實數向量空間 中序列緊致集合的定理。波爾查諾-魏爾斯特拉斯定理的核心部分可以僅僅使用序列的語言來表示:
中序列緊致集合的定理。波爾查諾-魏爾斯特拉斯定理的核心部分可以僅僅使用序列的語言來表示:
定理1:
任一 中的有界序列
中的有界序列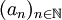 都至少包含一個收斂的子列。
都至少包含一個收斂的子列。
從這個定理出發,在給定的有界閉集F中任取一個序列,那麼這個序列是有界的,從而至少包含一個收斂的子列。而從F的封閉性可知,這個子列作為F的一部分,其收斂的極限必然也在F中。所以可以推知:
推論:
任一 中的有界閉集必然序列緊致。
中的有界閉集必然序列緊致。
這個推論給出了 中集合序列緊致的充分條件。另一方面,可以證明序列緊致的集合必然是有界閉集。這樣就將充分條件推進為充要條件:
中集合序列緊致的充分條件。另一方面,可以證明序列緊致的集合必然是有界閉集。這樣就將充分條件推進為充要條件:
 中的一個子集E是序列緊致的,當且僅當E是有界閉集。
中的一個子集E是序列緊致的,當且僅當E是有界閉集。
由於有限維賦範向量空間都與裝備了歐幾里德範數的 同胚,所以以上的定理都可以擴展到任意有限維賦範向量空間。
同胚,所以以上的定理都可以擴展到任意有限維賦範向量空間。
證明的關鍵是定理的核心部分,也就是定理1:任一 中的有界序列
中的有界序列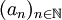 都至少包含一個收斂的子列。
都至少包含一個收斂的子列。
引理:
任何實數列必然包含單調函數的子列。
引理的證明:
設有實數列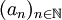 ,定義集合:
,定義集合: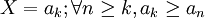 。集合中的每個元素,都比序列中排在其後的所有元素都大。
。集合中的每個元素,都比序列中排在其後的所有元素都大。
如果X中有無限個元素,在其中取下標遞增的一個數列,那麼這個數列是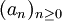 的子列,並且單調遞減,構造完畢。
的子列,並且單調遞減,構造完畢。
如果X中元素個數有限,那麼設N為X中元素的下標中最大的一個。對任意n > N,考慮an,an不在集合X中,所以an之後至少會有一個元素大於an。換句話說,序列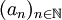 裡面排在aN後面的任一元素,它後面都必然還有一個比它大的元素。於是取k0 = N + 1,k1 > k0為第一個大於
裡面排在aN後面的任一元素,它後面都必然還有一個比它大的元素。於是取k0 = N + 1,k1 > k0為第一個大於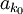 的元素的下標,k2 > k1為第一個大於
的元素的下標,k2 > k1為第一個大於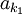 的元素的下標,依此類推,就可以得到
的元素的下標,依此類推,就可以得到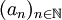 的一個單調遞增的子列。
的一個單調遞增的子列。
綜上可得,任何實數列必然包含單調的子列。
定理的證明:
先考慮一維(也就是n = 1)的情況。給定有界的實數列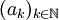 ,取它的一個單調子列。不妨設這個子列單調遞增,由於數列有上界,依據單調收斂定理#單調實數序列的收斂性|數列的單調收斂定理,這個子列必然收斂。
,取它的一個單調子列。不妨設這個子列單調遞增,由於數列有上界,依據單調收斂定理#單調實數序列的收斂性|數列的單調收斂定理,這個子列必然收斂。
對於高維(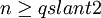 )的情況,證明的思路是取多次子列。
)的情況,證明的思路是取多次子列。
設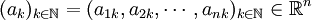 為一個有界序列,則n個實數列
為一個有界序列,則n個實數列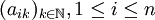 都是有界數列。於是存在
都是有界數列。於是存在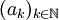 的子列
的子列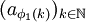 使得
使得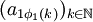 收斂。但是
收斂。但是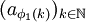 仍是有界數列,因而存在子列
仍是有界數列,因而存在子列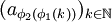 使得
使得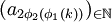 也收斂(註意這裡
也收斂(註意這裡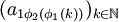 必然是收斂的)。在進行類似的n次操作後,我們就可以得到一個子列,使得
必然是收斂的)。在進行類似的n次操作後,我們就可以得到一個子列,使得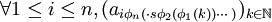 都收斂,也就是說存在子列
都收斂,也就是說存在子列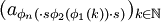 收斂。證畢。
收斂。證畢。
在有限維度量空間中,波爾查諾-魏爾斯特拉斯說明瞭序列緊致的集合就是有界閉集。然而在一般的度量空間中,有界閉集不一定是序列緊致的。為此,拓撲學中將一般度量空間中的序列緊致稱為波爾查諾-魏爾斯特拉斯性質。
定義:
設K為度量空間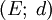 的子集。若K中任一序列
的子集。若K中任一序列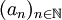 都包含一個收斂的子列,其極限也是K中元素,就稱K具有波爾查諾-魏爾斯特拉斯性質。
都包含一個收斂的子列,其極限也是K中元素,就稱K具有波爾查諾-魏爾斯特拉斯性質。
如果度量空間本身滿足波爾查諾-魏爾斯特拉斯性質,就稱這個度量空間為緊空間。在測度空間中,波爾查諾-魏爾斯特拉斯性質等價於海恩-波萊爾性質:所有K的開覆蓋都有限集合覆蓋。







