波尔查诺-魏尔斯特拉斯定理
出自 MBA智库百科(https://wiki.mbalib.com/)
目录 |
波尔查诺-魏尔施特拉斯定理是指数学拓扑学与实分析中用以刻划 中的紧集的基本定理,得名于数学家伯纳德•波尔查诺与卡尔•魏尔施特拉斯。波尔查诺-魏尔斯特拉斯定理说明,有限维实数|实向量空间
中的紧集的基本定理,得名于数学家伯纳德•波尔查诺与卡尔•魏尔施特拉斯。波尔查诺-魏尔斯特拉斯定理说明,有限维实数|实向量空间 中的一个子集E是紧集序列(每个序列都有收敛子序列)当且仅当E是有界闭集。
中的一个子集E是紧集序列(每个序列都有收敛子序列)当且仅当E是有界闭集。
这个定理最早由伯纳德•波尔扎诺证明,当他在证明介值定理时,附带证明了这个定理,但是他的证明已经散佚。卡尔•魏尔施特拉斯独自发现并证明了这个定理。波尔扎诺-魏尔施特拉斯定理是实分析中的基本定理。
子列:也称为子序列。一个序列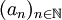 的一个子列是指在
的一个子列是指在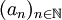 中抽取无穷多个元素,然后按照它们在原来序列里的顺序排列起来的序列。严格的定义是:如果存在一个从
中抽取无穷多个元素,然后按照它们在原来序列里的顺序排列起来的序列。严格的定义是:如果存在一个从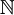 到
到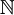 的严格单调递增的映射φ,使得
的严格单调递增的映射φ,使得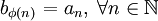 ,就称
,就称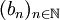 是
是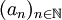 的一个子列。
的一个子列。
有界闭集: 中的有界闭集概念建立在给定的拓扑和度量上的。由于在有限维向量空间中所有度量等价,所以可以将
中的有界闭集概念建立在给定的拓扑和度量上的。由于在有限维向量空间中所有度量等价,所以可以将 视为装备了欧几里德度量的度量空间(并且可以定义相应的范数)。
视为装备了欧几里德度量的度量空间(并且可以定义相应的范数)。 的子集E有界,当且仅当所有E中元素x的范数小于一个给定常数K。注意这时对应的拓扑是欧几里德范数诱导的自然拓扑。
的子集E有界,当且仅当所有E中元素x的范数小于一个给定常数K。注意这时对应的拓扑是欧几里德范数诱导的自然拓扑。
序列紧致:称一个集合S是序列紧致的,是指每个由集合S中元素所组成的数列都包含极限(序列)|收敛的子列,并且该子列收敛到集合S中的某个元素。
波尔查诺-魏尔斯特拉斯定理可以视为刻画有限维实数向量空间 中序列紧致集合的定理。波尔查诺-魏尔斯特拉斯定理的核心部分可以仅仅使用序列的语言来表示:
中序列紧致集合的定理。波尔查诺-魏尔斯特拉斯定理的核心部分可以仅仅使用序列的语言来表示:
定理1:
任一 中的有界序列
中的有界序列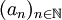 都至少包含一个收敛的子列。
都至少包含一个收敛的子列。
从这个定理出发,在给定的有界闭集F中任取一个序列,那么这个序列是有界的,从而至少包含一个收敛的子列。而从F的封闭性可知,这个子列作为F的一部分,其收敛的极限必然也在F中。所以可以推知:
推论:
任一 中的有界闭集必然序列紧致。
中的有界闭集必然序列紧致。
这个推论给出了 中集合序列紧致的充分条件。另一方面,可以证明序列紧致的集合必然是有界闭集。这样就将充分条件推进为充要条件:
中集合序列紧致的充分条件。另一方面,可以证明序列紧致的集合必然是有界闭集。这样就将充分条件推进为充要条件:
 中的一个子集E是序列紧致的,当且仅当E是有界闭集。
中的一个子集E是序列紧致的,当且仅当E是有界闭集。
由于有限维赋范向量空间都与装备了欧几里德范数的 同胚,所以以上的定理都可以扩展到任意有限维赋范向量空间。
同胚,所以以上的定理都可以扩展到任意有限维赋范向量空间。
证明的关键是定理的核心部分,也就是定理1:任一 中的有界序列
中的有界序列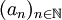 都至少包含一个收敛的子列。
都至少包含一个收敛的子列。
引理:
任何实数列必然包含单调函数的子列。
引理的证明:
设有实数列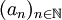 ,定义集合:
,定义集合: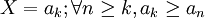 。集合中的每个元素,都比序列中排在其后的所有元素都大。
。集合中的每个元素,都比序列中排在其后的所有元素都大。
如果X中有无限个元素,在其中取下标递增的一个数列,那么这个数列是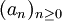 的子列,并且单调递减,构造完毕。
的子列,并且单调递减,构造完毕。
如果X中元素个数有限,那么设N为X中元素的下标中最大的一个。对任意n > N,考虑an,an不在集合X中,所以an之后至少会有一个元素大于an。换句话说,序列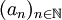 里面排在aN后面的任一元素,它后面都必然还有一个比它大的元素。于是取k0 = N + 1,k1 > k0为第一个大于
里面排在aN后面的任一元素,它后面都必然还有一个比它大的元素。于是取k0 = N + 1,k1 > k0为第一个大于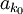 的元素的下标,k2 > k1为第一个大于
的元素的下标,k2 > k1为第一个大于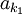 的元素的下标,依此类推,就可以得到
的元素的下标,依此类推,就可以得到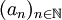 的一个单调递增的子列。
的一个单调递增的子列。
综上可得,任何实数列必然包含单调的子列。
定理的证明:
先考虑一维(也就是n = 1)的情况。给定有界的实数列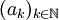 ,取它的一个单调子列。不妨设这个子列单调递增,由于数列有上界,依据单调收敛定理#单调实数序列的收敛性|数列的单调收敛定理,这个子列必然收敛。
,取它的一个单调子列。不妨设这个子列单调递增,由于数列有上界,依据单调收敛定理#单调实数序列的收敛性|数列的单调收敛定理,这个子列必然收敛。
对于高维(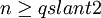 )的情况,证明的思路是取多次子列。
)的情况,证明的思路是取多次子列。
设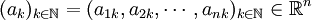 为一个有界序列,则n个实数列
为一个有界序列,则n个实数列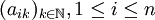 都是有界数列。于是存在
都是有界数列。于是存在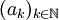 的子列
的子列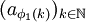 使得
使得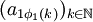 收敛。但是
收敛。但是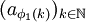 仍是有界数列,因而存在子列
仍是有界数列,因而存在子列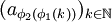 使得
使得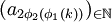 也收敛(注意这里
也收敛(注意这里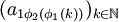 必然是收敛的)。在进行类似的n次操作后,我们就可以得到一个子列,使得
必然是收敛的)。在进行类似的n次操作后,我们就可以得到一个子列,使得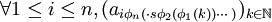 都收敛,也就是说存在子列
都收敛,也就是说存在子列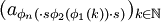 收敛。证毕。
收敛。证毕。
在有限维度量空间中,波尔查诺-魏尔斯特拉斯说明了序列紧致的集合就是有界闭集。然而在一般的度量空间中,有界闭集不一定是序列紧致的。为此,拓扑学中将一般度量空间中的序列紧致称为波尔查诺-魏尔斯特拉斯性质。
定义:
设K为度量空间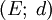 的子集。若K中任一序列
的子集。若K中任一序列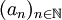 都包含一个收敛的子列,其极限也是K中元素,就称K具有波尔查诺-魏尔斯特拉斯性质。
都包含一个收敛的子列,其极限也是K中元素,就称K具有波尔查诺-魏尔斯特拉斯性质。
如果度量空间本身满足波尔查诺-魏尔斯特拉斯性质,就称这个度量空间为紧空间。在测度空间中,波尔查诺-魏尔斯特拉斯性质等价于海恩-波莱尔性质:所有K的开覆盖都有限集合覆盖。







