曼-惠特尼U檢驗
出自 MBA智库百科(https://wiki.mbalib.com/)
曼-惠特尼U檢驗(Mann-Whitney U test)
目錄 |
曼-惠特尼U檢驗又稱“曼-惠特尼秩和檢驗”,是由H.B.Mann和D.R.Whitney於1947年提出的。它假設兩個樣本分別來自除了總體均值以外完全相同的兩個總體,目的是檢驗這兩個總體的均值是否有顯著的差別。
曼-惠特尼秩和檢驗可以看作是對兩均值之差的參數檢驗方式的T檢驗或相應的大樣本正態檢驗的代用品。由於曼-惠特尼秩和檢驗明確地考慮了每一個樣本中各測定值所排的秩,它比符號檢驗法使用了更多的信息。
曼-惠特尼U檢驗的步驟 [1]
曼-惠特尼U檢驗的步驟是:
1.從兩個總體A和B中隨機抽取容量為nA和nB的兩個獨立隨機樣本,將(nA + nB)個觀察值按大小順序排列,指定1為最小(或最大)觀察值,指定2為第二個最小(或第二個最大)的觀察值,依此類推。如果存在相同的觀察值,則用它們位序的平均數。
2.計算兩個樣本的等級和TA和TB。
3.根據TA和TB即可給出曼-惠特尼U檢驗的公式。計算得到的兩個U值不相等,但是它們的和總是等於nAnB,即有UA + UB = nAnB。若 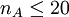 、
、 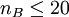 時,則其檢驗統計量為:
時,則其檢驗統計量為:
UA = nAnB + nA(nA + 1) / 2 − TA
UB = nAnB + nB(nB + 1) / 2 − TB
在檢驗時,因為曼-惠特尼U檢驗的臨界值表只給出了較小的臨界值,所以用UA、UB中較小的U值作為檢驗統計量。
4.選擇其中較小U值與U的臨界值比較,若U大於Uα,接受原假設H0,若U小於Uα則拒絕H0,接受H1。接受域與威爾科克森檢驗相同。U檢驗也有小樣本和大樣本之分,在小樣本時,U的臨界值均已編製成表。在大樣本時,U的分佈趨近正態分佈,因此可用正態逼近處理。
下麵是兩種不同加工方式的菜粕在黃牛瘤胃內培養16h的乾物質降解率,用曼-惠特尼U檢驗比較其有無差異:
兩種加工方式的菜粕瘤胃培養16h的乾物質降解率(%)
| 預壓浸出組 | 等級排序 | 螺旋熱榨組 | 等級排序 |
|---|---|---|---|
| 39.33 | 3 | 42.91 | 5 |
| 44.10 | 8 | 44.69 | 10 |
| 35.89 | 1 | 44.54 | 9 |
| 43.35 | 6 | 45.31 | 11 |
| 47.61 | 13 | 37.73 | 2 |
| 43.71 | 7 | 48.75 | 14 |
| 46.71 | 12 | ||
| 41.85 | 4 |
先按照大小順序排列等級(見上表),而後計算TA = 38,TB = 67,n1 = 6,n2 = 8。
假設兩種菜粕的16h瘤胃乾物質降解率除了平均水平以外在其它方面無差異,即檢驗:
- H0:兩種菜粕的16h瘤胃乾物質降解率無差異;
- H1:兩種菜粕的16h瘤胃乾物質降解率有差異。
計算U值:
U2值較小,選取U2與Uα(α=0.05)比較,通過查表(附表)可知Uα = 8,U2 > Uα,即接受H0,認為兩種加工方式的菜粕瘤胃培養16h的乾物質降解率無顯著差異。
附表:
曼-惠特尼檢驗U的臨界值表
(僅列出單側檢驗在0.025或雙側檢驗在0.05處的U臨界值)
| n2 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| n1 | |||||||||||||||
| 1 | |||||||||||||||
| 2 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | |||||||
| 3 | 0 | 1 | 1 | 2 | 2 | 3 | 3 | 4 | 4 | 5 | 5 | ||||
| 4 | 0 | 1 | 2 | 3 | 4 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |||
| 5 | 0 | 1 | 2 | 3 | 5 | 6 | 7 | 8 | 9 | 11 | 12 | 13 | 14 | ||
| 6 | 1 | 2 | 3 | 5 | 6 | 8 | 10 | 11 | 13 | 14 | 16 | 17 | 19 | ||
| 7 | 1 | 3 | 5 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 | 24 | ||
| 8 | 0 | 2 | 4 | 6 | 8 | 10 | 13 | 15 | 17 | 19 | 22 | 24 | 26 | 29 | |
| 9 | 0 | 2 | 4 | 7 | 10 | 12 | 15 | 17 | 20 | 23 | 26 | 28 | 31 | 34 | |
| 10 | 0 | 3 | 5 | 8 | 11 | 14 | 17 | 20 | 23 | 26 | 29 | 33 | 36 | 39 | |
| 11 | 0 | 3 | 6 | 9 | 13 | 16 | 19 | 23 | 26 | 30 | 33 | 37 | 40 | 44 | |
| 12 | 1 | 4 | 7 | 11 | 14 | 18 | 22 | 26 | 29 | 33 | 37 | 41 | 45 | 49 | |
| 13 | 1 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 33 | 37 | 41 | 45 | 50 | 54 | |
| 14 | 1 | 5 | 9 | 13 | 17 | 22 | 26 | 31 | 36 | 40 | 45 | 50 | 55 | 59 | |
| 15 | 1 | 5 | 10 | 14 | 19 | 24 | 29 | 34 | 39 | 44 | 49 | 54 | 59 | 64 |
- ↑ 孫允午.統計學:數據的搜集、整理和分析.上海財經大學出版社,2006年02月第1版
評論(共15條)
我也跟樓上有同樣的疑惑,感覺到第三步就應該完了吧,如果拒絕了H0,接收H1,就說明兩序列差異明顯。如果接受H0,就表明兩序列差異不明顯。整個過程就應該完了啊。
上面那個方法是對n1和n2都小於或等於10的情況下的計算方法,但是大部分時候n1和n2都是大於10的。這時候上面那個方法就行不通了,需要另外一種,上面沒有講全。
上面那個方法是對n1和n2都小於或等於10的情況下的計算方法,但是大部分時候n1和n2都是大於10的。這時候上面那個方法就行不通了,需要另外一種,上面沒有講全。
MBA智庫百科是可以自由參與的百科,如有發現錯誤和不足,您也可以參與修改編輯,期待您的加入!
你的努力是大家都可看得到。但要提醒一點:中國所謂的“大家”寫的書往往也是抄來抄去,最後也不知道抄誰的,就算從中文統計學書中搬來,但其書本就說錯了,搬來當然就不對,中國多本統計書都是這麼寫,但看英文同條目裡人家參考文獻直接是提出該檢驗方法的幾位作者。如,魏鳳英的《現代氣候統計診斷與預測技術》提的幾種檢驗方法和唐啟義的《DPS數據處理系統》書中同樣方法都有出入,與原作者提出都不一樣,兩書都出了好幾個版本
US wiki posted a different calculating method other than this one. I found this same equation in the Japan wiki.
在最後的臨界值表中,n1=1,和n2=1的時候都為空,n1=2和n2=2的部分為空,是表示樣本太小無法計算嗎?
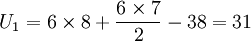
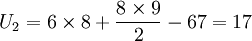








很詳細, 謝謝!