戴爾指數
出自 MBA智库百科(https://wiki.mbalib.com/)
戴爾指數(Theil Index)是一個衡量經濟不平等的統計量,由計量經濟學家亨利·戴爾導出的。
目錄 |
其公式為
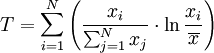
其中xi為第i個人的收入,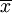 為平均收入,N為人口數量。加總符號中的第一項可以理解為個人在總收入中所占的比例,第二項為該個人相對於均值的收入。如果每一個人都有相同的收入,即等於均值,則指數為零。如果某個個人擁有所有的收入,則指數為lnN。
為平均收入,N為人口數量。加總符號中的第一項可以理解為個人在總收入中所占的比例,第二項為該個人相對於均值的收入。如果每一個人都有相同的收入,即等於均值,則指數為零。如果某個個人擁有所有的收入,則指數為lnN。
戴爾指數導自Claude Shannon的信息熵測度。設T為戴爾指數,S為Shannon的測度,則有
T = ln(N) − S
Shannon根據事件發生概率導出的其熵測度。它可以用戴爾繫數解釋為自某個特定個人處隨機取得一塊錢的概率。並與其第一項,即總收入中個人所占份額相同。
戴爾指數的一個優點是它是某個子群體中不平等的加權和。例如,美國國內的不平等就是每個州的不平等的加權和,由該州收入相對於國家總收入的比值來加權。
如果人口被劃分為m個子群體,sk為群體k的收入比例,Tk為該子群體的戴爾指數,而 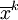 為子群體 k的平均收入,則戴爾指數為
為子群體 k的平均收入,則戴爾指數為
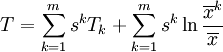
因此,我們可以說某個特定群體給總體“貢獻了”一定數量的不平等。
另外一個被廣泛使用的不平等度量為基尼繫數,該繫數對於很多人來說由於基於勞倫斯曲線而非常直觀。但是它卻沒有戴爾指數來得容易分解。
德克薩斯大學戴爾指數簡介(英文)








Strengths: - symmetric: invariance under permutations of individuals - replication invariant: independent of population replications - mean independent: invariant under scalar multiplication of income - decomposable