總體回歸函數

出自 MBA智库百科(https://wiki.mbalib.com/)

　　進行回歸分析通常要設定一定的數學模型。在回歸分析中，最簡單的模型是只有一個因變數和一個自變數的線性回歸模型。這一類模型就是一元線性回歸模型，又稱簡單線性回歸模型。

　　該類模型假定因變數Y主要受自變數X的影響，它們之間存在著近似的

　　線性函數關係，即有：

　　Y_t = β1 + β2X_t + U_t （1-1）

　　(1-1)式被稱為總體回歸函數。

　　式中，β1、β2是未知的參數，又叫回歸繫數

　　Yt和Xt分別是Y和X的第t次觀測值。

　　Ut是隨機誤差項，又稱隨機干擾項，它是一個特殊的隨機變數，反映未列入方程式的其他各種因素對Y的影響。

　　1.總體回歸直線是未知的，且只有一條。而樣本回歸直線是已知的，且可以有許多條（從總體中可以取許多樣本，每抽取一組樣本，便可以擬合一條直線）。

　　2.總體回歸函數中β1、β2是未知參數，表現為常數；而樣本回歸函數中的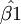和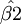是隨機變數，其具體數值隨所抽取的樣本觀測值不同而不同。

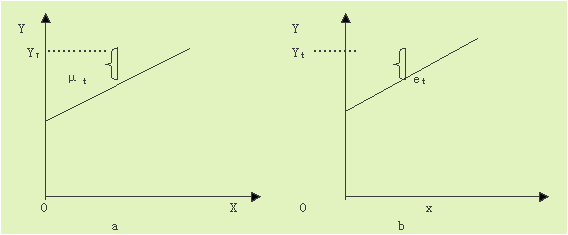
　　3.總體回歸函數中的ut是Yt與未知總體回歸直線之間的縱向距離，它是不可直接觀測的；而樣本回歸函數中的et是Yt與樣本回歸直線之間的縱向距離，當根據樣本觀測值擬合出樣本回歸直線後，可以計算出et的具體數值。ut和et在各自直線上的位置分別見下圖a和b所示。