总体回归函数

出自 MBA智库百科(https://wiki.mbalib.com/)

　　进行回归分析通常要设定一定的数学模型。在回归分析中，最简单的模型是只有一个因变量和一个自变量的线性回归模型。这一类模型就是一元线性回归模型，又称简单线性回归模型。

　　该类模型假定因变量Y主要受自变量X的影响，它们之间存在着近似的

　　线性函数关系，即有：

　　Y_t = β1 + β2X_t + U_t （1-1）

　　(1-1)式被称为总体回归函数。

　　式中，β1、β2是未知的参数，又叫回归系数

　　Yt和Xt分别是Y和X的第t次观测值。

　　Ut是随机误差项，又称随机干扰项，它是一个特殊的随机变量，反映未列入方程式的其他各种因素对Y的影响。

　　1.总体回归直线是未知的，且只有一条。而样本回归直线是已知的，且可以有许多条（从总体中可以取许多样本，每抽取一组样本，便可以拟合一条直线）。

　　2.总体回归函数中β1、β2是未知参数，表现为常数；而样本回归函数中的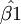和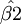是随机变量，其具体数值随所抽取的样本观测值不同而不同。

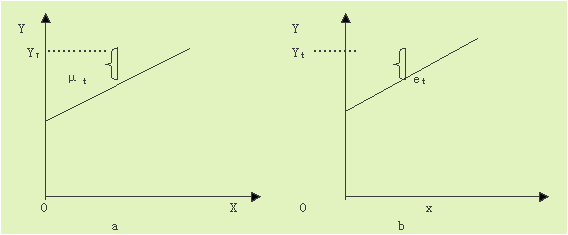
　　3.总体回归函数中的ut是Yt与未知总体回归直线之间的纵向距离，它是不可直接观测的；而样本回归函数中的et是Yt与样本回归直线之间的纵向距离，当根据样本观测值拟合出样本回归直线后，可以计算出et的具体数值。ut和et在各自直线上的位置分别见下图a和b所示。