完美信息博弈
出自 MBA智库百科(https://wiki.mbalib.com/)
- 完美信息博弈(Games With Perfect Information)
目錄 |
完全信息動態博弈可分為完全完美信息動態博弈和完全不完美信息動態博弈。[1]
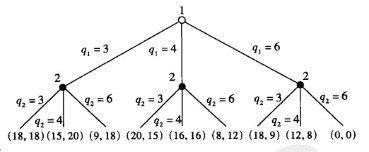
完美信息博弈是一個有趣的特例,在這類博弈中所有的信息集都是單點集。在完美信息博弈中,每時點參與人採取一個行動,每個參與人在其決策的同時知道以前所有的行動。斯塔克伯格博弈就是完美信息博弈。下圖表示了一種博弈樹,該博弈樹假設每一個參與人只有三種可能的產出水平:3,4和6。樹中每一分枝末端的向量分別是參與人1和參與人2的收益水平。[2]
虛擬的完美信息博弈[3]
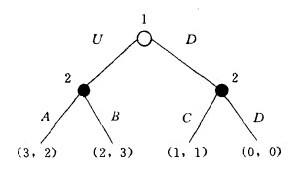
下圖就是一個虛擬的完美信息博弈。
該博弈樹有兩個倒數第二個結,且均為局中人2的決策結。在四種可能結局中,局中人2取B,則獲最高盈利3。也可能存在這樣的現象,對該局中人來說,有兩個或兩個以上的結局都使他獲得同樣的最高盈利,稱為存在“結”(tie)現象(註:此結與博弈樹中的結(node)有著本質差異),那麼可以在其中任意選擇一個行動。現在在給定處於倒數第二結的局中人採取我們剛纔已確定的行動前提下,確定在其直接後續結是倒數第二結的那些結上的每一個局中人選擇一個在可行後續結上盈利為極大的行動。這樣我們可以通過博弈樹一步一步地往後退,在每個結上為該行動的局中人選定行動。事實上,我們已經為每一個局中人確定了一個策略。這些策略形成了一個Nash均衡(註:這裡沒有證明它是Nash均衡)。這裡敘述的辦法(數學上稱為Zermelo演算法)與後退歸納有所區別,Zermelo演算法在沿博弈樹後退過程在每一個結為每一個局中人確定其最大可能盈利的行動,實際上Zermelo演算法是後退歸納法的多人(n>2)博弈推廣。
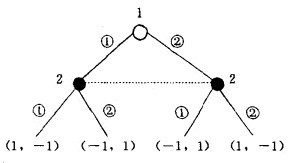
如果“完美信息的有限博弈具有一個純策略Nash均衡”條件不滿足的話,Zermelo演算法就難以有所作為。例如,如果將有限博弈改為無限博弈,無非是要麼具有一個單一結,在它後面有無限多個後續結(譬如博弈具有連續統的行動空間),要麼博弈具有一條由無限多個結組成的路徑。在後一種無限博弈情況,不存在倒數第二結,故無法談論Zermelo演算法;在第一種情況,如果對盈利函數沒有進一步限制的話則不存在最佳選擇,簡單地說,即使行動空間是[0,1]這樣具連續統勢的閉區間。並不是說[0,1]上的函數一定存在極大值,必須要對盈利函數加上適當的條件。其次,如果定理條件中的完美信息改為不完美信息的話,設想倒數第二結相應的信息集不完美,處於該信息集的局中人無法知道自己處於哪個決策結,縱然信息是完全的(即他對各結局的盈利向量一清二楚),他還是不能為自己確定一個最佳行動。最簡單的例子是猜謎博弈,由於兩個局中人同時行動,因此信息不完美,繪製博弈樹如下圖,圖中枝旁小圓圈中的數字表示行動中伸出的手指數。
倒數第二結是局中人2的決策結,共有2個。但它們構成局中人2的不完美信息集,局中人2的可能最高盈利為l,可是由於他不知道局中人l伸出幾根手指,因此他確定不了自己伸出多少根手指為最佳選擇。事實上,我們已經知道,猜謎博弈不存在純策略Nash均衡。