完美信息博弈
出自 MBA智库百科(https://wiki.mbalib.com/)
- 完美信息博弈(Games With Perfect Information)
目录 |
完全信息动态博弈可分为完全完美信息动态博弈和完全不完美信息动态博弈。[1]
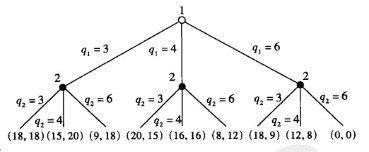
完美信息博弈是一个有趣的特例,在这类博弈中所有的信息集都是单点集。在完美信息博弈中,每时点参与人采取一个行动,每个参与人在其决策的同时知道以前所有的行动。斯塔克伯格博弈就是完美信息博弈。下图表示了一种博弈树,该博弈树假设每一个参与人只有三种可能的产出水平:3,4和6。树中每一分枝末端的向量分别是参与人1和参与人2的收益水平。[2]
虚拟的完美信息博弈[3]
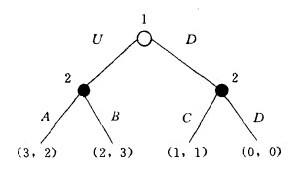
下图就是一个虚拟的完美信息博弈。
该博弈树有两个倒数第二个结,且均为局中人2的决策结。在四种可能结局中,局中人2取B,则获最高盈利3。也可能存在这样的现象,对该局中人来说,有两个或两个以上的结局都使他获得同样的最高盈利,称为存在“结”(tie)现象(注:此结与博弈树中的结(node)有着本质差异),那么可以在其中任意选择一个行动。现在在给定处于倒数第二结的局中人采取我们刚才已确定的行动前提下,确定在其直接后续结是倒数第二结的那些结上的每一个局中人选择一个在可行后续结上盈利为极大的行动。这样我们可以通过博弈树一步一步地往后退,在每个结上为该行动的局中人选定行动。事实上,我们已经为每一个局中人确定了一个策略。这些策略形成了一个Nash均衡(注:这里没有证明它是Nash均衡)。这里叙述的办法(数学上称为Zermelo算法)与后退归纳有所区别,Zermelo算法在沿博弈树后退过程在每一个结为每一个局中人确定其最大可能盈利的行动,实际上Zermelo算法是后退归纳法的多人(n>2)博弈推广。
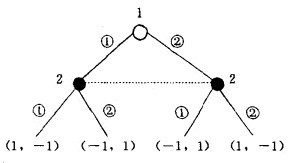
如果“完美信息的有限博弈具有一个纯策略Nash均衡”条件不满足的话,Zermelo算法就难以有所作为。例如,如果将有限博弈改为无限博弈,无非是要么具有一个单一结,在它后面有无限多个后续结(譬如博弈具有连续统的行动空间),要么博弈具有一条由无限多个结组成的路径。在后一种无限博弈情况,不存在倒数第二结,故无法谈论Zermelo算法;在第一种情况,如果对盈利函数没有进一步限制的话则不存在最佳选择,简单地说,即使行动空间是[0,1]这样具连续统势的闭区间。并不是说[0,1]上的函数一定存在极大值,必须要对盈利函数加上适当的条件。其次,如果定理条件中的完美信息改为不完美信息的话,设想倒数第二结相应的信息集不完美,处于该信息集的局中人无法知道自己处于哪个决策结,纵然信息是完全的(即他对各结局的盈利向量一清二楚),他还是不能为自己确定一个最佳行动。最简单的例子是猜谜博弈,由于两个局中人同时行动,因此信息不完美,绘制博弈树如下图,图中枝旁小圆圈中的数字表示行动中伸出的手指数。
倒数第二结是局中人2的决策结,共有2个。但它们构成局中人2的不完美信息集,局中人2的可能最高盈利为l,可是由于他不知道局中人l伸出几根手指,因此他确定不了自己伸出多少根手指为最佳选择。事实上,我们已经知道,猜谜博弈不存在纯策略Nash均衡。