多普勒效應

出自 MBA智库百科(https://wiki.mbalib.com/)

　　多普勒效應指出，波在波源移向觀察者接近時接收頻率變高，而在波源遠離觀察者時接收頻率變低。當觀察者移動時也能得到同樣的結論。但是由於缺少實驗設備，多普勒當時沒有用實驗驗證，幾年後有人請一隊小號手在平板車上演奏，再請訓練有素的音樂家用耳朵來辨別音調的變化，以驗證該效應。假設原有波源的波長為λ，波速為c，觀察者移動速度為v：

　　當觀察者走近波源時觀察到的波源頻率為（c+v）/λ，反之則觀察到的波源頻率為（c-v）/λ。

　　一個常被使用的例子是火車的汽笛聲，當火車接近觀察者時，如果觀察者遠離波源，其汽鳴聲會比平常更刺耳。你可以在火車經過時聽出刺耳聲的變化。同樣的情況還有：警車的警報聲和賽車的發動機聲。

　　如果把聲波視為有規律間隔發射的脈衝，可以想象若你每走一步，便發射了一個脈衝，那麼在你之前的每一個脈衝都比你站立不動時更接近你自己。而在你後面的聲源則比原來不動時遠了一步。或者說，在你之前的脈衝頻率比平常變高，而在你之後的脈衝頻率比平常變低了。

　　觀察者 (Observer) 和發射源 (Source) 的頻率關係為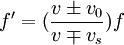： 　　f'為觀察到的頻率；

　　f為發射源於該介質中的原始發射頻率；

　　v為波在該介質中的行進速度；

　　v₀為觀察者移動速度，若接近發射源則前方運算符號為 + 號, 反之則為 - 號；

　　v_s為發射源移動速度，若接近觀察者則前方運算符號為 - 號，反之則為 + 號。

　　通過這個公式，我們就知道火車接近你的時候音調變化的原因：公式中分子是聲音傳播速度和觀察者速度之和（v+v₀），分母是聲音傳播速度和火車速度之差（v-v_s），然後和聲源原始頻率（f）進行乘法運算。觀察者接受到的頻率f'比火車笛聲的原始頻率變高，所以聽到的火車鳴笛音調變高。反之，當觀察者和火車遠離的時候，分子減法運算變小，分母加法運算變大，計算得到的頻率比火車鳴笛的原始聲音頻率變低，故聽到音調變低。

　　產生原因：聲源完成一次全振動，向外發出一個波長的波，頻率表示單位時間內完成的全振動的次數，因此波源的頻率等於單位時間內波源發出的完全波的個數，而觀察者聽到的聲音的音調，是由觀察者接受到的頻率，即單位時間接收到的完全波的個數決定的。當波源和觀察者有相對運動時，觀察者接收到的頻率會改變．在單位時間內，觀察者接收到的完全波的個數增多，即接收到的頻率增大．同樣的道理，當觀察者遠離波源，觀察者在單位時間內接收到的完全波的個數減少，即接收到的頻率減小．

　　多普勒效應Doppler effect是為紀念奧地利物理學家及數學家克裡斯琴·約翰·多普勒（Christian Johann Doppler）而命名的，他於1842年首先提出了這一理論。主要內容為物體輻射的波長因為波源和觀測者的相對運動而產生變化。在運動的波源前面，波被壓縮，波長變得較短，頻率變得較高（藍移blue shift）；在運動的波源後面時，會產生相反的效應。波長變得較長，頻率變得較低（紅移red shift）；波源的速度越高，所產生的效應越大。根據波紅（藍）移的程度，可以計算出波源循著觀測方向運動的速度。

　　恆星光譜線的位移顯示恆星循著觀測方向運動的速度，除非波源的速度非常接近光速，否則多普勒位移的程度一般都很小。所有波動現象都存在多普勒效應。

　　雖然不像蘋果砸到牛頓頭上，激發“萬有引力”的靈感那麼神奇，多普勒效應也是一個偶然的發現。1842年奧地利一位名叫多普勒的數學家、物理學家。一天，他正路過鐵路交叉處，恰逢一列火車從他身旁馳過，他發現火車從遠而近時汽笛聲變響，音調變尖，而火車從近而遠時汽笛聲變弱，音調變低。他對這個物理現象感到極大興趣，併進行了研究。發現這是由於振源與觀察者之間存在著相對運動，使觀察者聽到的聲音頻率不同於振源頻率的現象。這就是頻移現象。因為，聲源相對於觀測者在運動時，觀測者所聽到的聲音會發生變化。當聲源離觀測者而去時，聲波的波長增加，音調變得低沉，當聲源接近觀測者時，聲波的波長減小，音調就變高。音調的變化同聲源與觀測者間的相對速度和聲速的比值有關。這一比值越大，改變就越顯著，後人把它稱為“多普勒效應”。

　　多普勒效應不僅僅適用於聲波，它也適用於所有類型的波，包括電磁波。科學家愛德文·哈勃（Edwin Hubble）使用多普勒效應得出宇宙正在膨脹的結論。他發現遠離銀河系的天體發射的光線頻率變低，即移向光譜的紅端，稱為紅移，天體離開銀河系的速度越快紅移越大，這說明這些天體在遠離銀河系。反之，如果天體正移向銀河系，則光線會發生藍移。

　　在移動通信中，當移動台移向基站時，頻率變高，遠離基站時，頻率變低，所以我們在移動通信中要充分考慮多普勒效應。當然，由於日常生活中，我們移動速度的局限，不可能會帶來十分大的頻率偏移，但是這不可否認地會給移動通信帶來影響，為了避免這種影響造成我們通信中的問題，我們不得不在技術上加以各種考慮。也加大了移動通信的複雜性。

　　在單色的情況下，我們的眼睛感知的顏色可以解釋為光波振動的頻率，或者解釋為，在1秒鐘內電磁場所交替為變化的次數。在可見區域，這種頻率越低，就越趨向於紅色，而頻率越高的，就趨向於藍,紫色。比如，由氦——氖激光所產生的鮮紅色對應的頻率為4.74×10^14赫茲，而汞燈的紫色對應的頻率則在7×10^14赫茲以上。這個原則同樣適用於聲波：聲音的高低的感覺對應於聲音對耳朵的鼓膜施加壓力的振動頻率（高頻聲音尖厲，低頻聲音低沉）。

　　如果波源是固定不動的，不動的接收者所接收的波的振動與波源發射的波的節奏相同：發射頻率等於接收頻率。如果波源相對於接收者來說是移動的，比如相互遠離，那麼情況就不一樣了。相對於接收者來說，波源產生的兩個波峰之間的距離拉長了，因此兩上波峰到達接收者所用的時間也變長了。那麼到達接收者時頻率降低，所感知的顏色向紅色移動（如果波源向接收者靠近，情況則相反）。為了讓讀者對這個效應的影響大小有個概念，在顯示了多普勒頻移，近似給出了一個正在遠離的光源在相對速度變化時所接收到的頻率。例如，在上面提到的氦——氖激光的紅色譜線，當波源的速度相當於光速的一半時，接收到的頻率由4.74×10^14赫茲下降到2.37×10^14赫茲，這個數值大幅度地降移到紅外線的頻段。