圖像數字化

出自 MBA智库百科(https://wiki.mbalib.com/)

　　一幅黑白靜止平面圖像（如照片）中各點的灰度值可用其位置坐標（x,y）的函數f（x，y）來描述。顯然f（x，y）是二維連續函數。有無窮多個取值。這種用連續函數表示的圖像無法用電腦進行處理，也無法在各種數字系統中傳輸或存儲。必須將代表圖像的連續（模擬）信號轉變為離散（數字）信號。這樣的變換過程，稱為圖像數字化。

　　圖像數字化的內容包括兩個方面:採樣和量化。

　　圖像在空間上的離散化稱為採樣。即使空間上連續變化的圖像離散化。也就是用空間上部分點的灰度值來表示圖像。這些點稱其為樣點（或像素、像元、樣本）。一幅圖像應取多少樣點呢?其約束條件是:由這些樣點，採用某種方法能夠正確重建原圖像。採樣的方法有兩類:一類是直接對錶示圖像的二維函數值進行採樣。即讀取各離散點上的信號值。所得結果就是一個樣點值陣列。所以也稱為點陣採樣。另一類是先將圖像函數進行某種正交變換，用其變換繫數作為採樣值，故稱為正交繫數採樣。

　　對樣點灰度級值的離散化過程稱為量化。也就是對每個樣點值數位化，使其只和有限個可能電平數中的一個對應，即使圖像的灰度級值離散化。量化也可以分為兩種:一種是將樣點灰度級值等間隔分檔取整，稱為均勻量化;另一種是不等間隔分檔取整，稱為非均勻量化。因為都要取整，故量化也常稱為整量或整量化過程。

　　假定一幅圖像取M*N個樣點，對樣點值進行Q級分檔取整。那麼對M,N和Q如何取值呢?

　　首先，M,N,Q一般總是取成2的整數次冪，如Q = 2^b,b為正整數。通常稱為對圖像進行b比特量化。M,N可以取成相等，也可以不相等。若取相等，則圖像矩陣為方陣，分析運算方便些。取不等的例子如陸地衛星圖像就因實際需要而取成2340*3240。

　　其次，關於M,N,b（或Q）數值大小的確定。對b來講，取值越大，重建圖像失真越小，若要完全不失真重建原圖像，b必須取無窮大，否則一定存在失真。這就是所謂量化誤差。一般供人眼觀察的圖像，由於人眼對灰度分辨能力有限，用5-8比特量化就可以了。而衛星照片、航空照片等為了區別圖像中灰度變化不大的目標，往往用8-12比特量化。對MyN的取值，主要依據是採樣的約束條件。也就是在M*N大到滿足採樣定理的情況下，重建圖像就不會產生失真，否則就會因採樣點數不夠而產生所謂混淆失真。為了減少表示圖像的比特數，總是取MXN點數剛好滿足採樣定理。這種狀態的採樣即所謂奈奎斯特採樣（如彩色電視編碼技術等）。M*N常用的尺寸有512*512,256*256,64*64,32*32等。

　　再次，在實際應用中，如果給定了允許表示圖像的總比特數M*N*b，對N*N和b的分配往往是根據圖像的內容和應用要求以及系統本身的技術指標來選定。例如，若圖像中有大面積灰度變化緩慢的平滑區域，如人頭像特寫照片等。則M*N採樣點數可以少些，而量化比特數h多些。這樣使重建圖像灰度層次多些。若b太少，在圖像灰度平滑區往往會出現“假輪廓”。反之，複雜的景物圖像，如群眾場面的照片等，量化比特數b可以少些而採樣點數M*N要多些。這樣不致丟失圖像的細節。究竟M*N和b如何組合才能獲

　　得滿意的結果，很難講出一個統一的方案。T.S.Huang研究了這個問題。他對三種不同特征的圖像（一幅細節少的婦女頭像特寫照片，一幅中等細節攝影師工作照片，一幅包含大量細節的群眾會場照片），改變其採樣點數M*N和量化比特數b，分別進行圖像質量的主觀評價。總的結論是:不同的採樣點數和量化比特數組合，可以獲得相同的主觀質量評價。

　　由各種不同的圖像感測器所獲取的圖像信號都是模擬量，為了能使其送往電腦或數字硬體進行運算處理，必須將這些模擬信號變為數字信號，這樣的過程稱為數字化，顯然，數字化應包括空間採樣、幅度量化和編碼三個主要部分。

　　—、採樣過程

　　根據資訊理論中的香農採樣定理，圖像信息的採樣周期是由圖像信號的上限頻率所決定的。而且輸入設備中的圖像信號放大器帶寬也受這個上限頻率制約。因此，首先要分析一下圖像信號的上限頻率。

　　1、圖像信號上限頻率計算

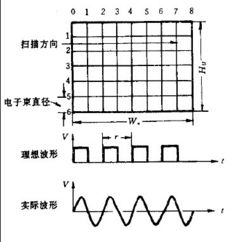
　　2、以電視圖像為例來說明圖像信號上限頻率的確定方法，見圖1。假設每一個小方格就是一個像素，而且.電子束正好和這些小方格重合，那麼掃描這些像素所得電信號的頻率就是圖像信號的最高頻率（即上限頻率）。

　　設圖像橫向長度為W_h，縱向長度為H_u，橫縱比為4/3。

　　設縱方向上有N'個像素，且縱橫方向分解力相等，則橫方向的像素數M應為: 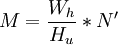，實際一幀圖像縱方向掃描行數N總是大於N'。這是因為有場消隱行數的存在。故要乘一個繫數k_u，另外由於掃描線與像素間相對位置影響，還要乘一個繫數k（也稱垂直分解力繫數）。因此，N’和N關係如下:

　　N' = k * k_u * N

　　式中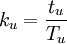,t_u為場掃描正程時間，T_u為場掃描周期。由此可以求出水平方向所能傳送的像素數M。

　　設T_h為行掃描周期，t_h為行掃正程時間，那麼橫方向每一個像素所需時間T為:

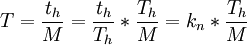
　　從圖1可以看出圖像信號的最小周期應是掃描過二個方格（像素）所需要的時間，那麼其倒數即為圖像的最高頻率f_max：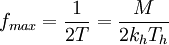

　　設幀周期為T_p，幀頻為f_p，那麼

　　T_h = T_p / N = 1 / Nf_p

　　則最高圖像頻率f_max應為f_max==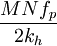

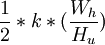
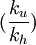
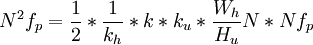
　　我國電視制式，N=625, f_p = 25，場周期20ms，場回掃1.6ms,行周期為64us，行回掃為11.8-12us，那麼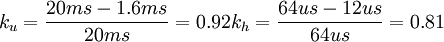

　　一般情況下k取0.7-0.8, W_u / H_h = 4 / 3。代入上式即可求出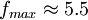MHz其它的掃描方式輸入圖像信號一最高頻率計算原理方法是一樣的。

　　2.採樣預率的計算

　　有一了圖像信號的最高頻率f_max,不丟失信息的採樣頻率f_s應大

　　於或等於2f_max採樣周期t_s應小於或等於1 / 2f_max。對625行50場

　　電視制式的圖像其採樣周期t為:

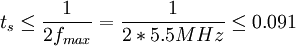　　us

　　t_s是理淪計算結果，實際工程應用兼顧設備價格，往往取稍大於t_s，從理論上講不滿足採樣定理，就會產生混淆失真，但實際應用中，這樣的圖像質量是允許的。例如取t_s = 0.125us，稍大於0.091us，但此採樣頻率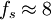MHz，可以直接山行頻分頻而來，這就方便多了。再如圖像處理系統中，為了運算方便，往往把圖像解析度取為512*512，則採樣周期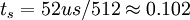us,即採樣頻率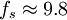MHz。

　　一般情況下是完全能夠滿足要求的。

　　3.採樣點數的計算

　　下麵我們再分析一下採樣點數，仍以電視圖像為例。為了減少視頻信號帶寬，一般電視採用隔行掃描，即分奇數場和偶數場，對625行電視系統來講每場有312.5行。場消隱每場25行，因此實際有效行數為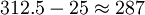行。若採用方格採樣，每場行方向最多只能取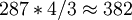點，也就是講若只對一場（奇數場或偶數場）採樣，最大採樣點數為287*382點。可見一般圖像處理中使用512*512採樣點陣，就必須對一幀中的兩場採樣。

　　4.採樣方式的選擇

　　圖像信號採樣方式在一般情況下多採用點陣採樣，就是直接對錶示圖像的二維函數值進行採樣，讀取圖像函數空間各離散點的值，所得結果就是一個樣點值陣列，故稱為點陣採樣。點陣採樣可以是正方格（行和列等間隔取樣點且呈正方格排列）順序採樣;也可以是針對電視圖像的隔行採樣;還可以是縱向採樣，即每行採一點，一場採一列。點陣採樣另一種是正交採樣（也稱平行四邊形採樣或六角形採樣）即相鄰行的採樣點呈正交分佈。採樣方式的選擇是由圖像信息的應用要求決定的，分別扼要地介紹如下。

　　（1）正方格順序採樣:

　　正方格順序採樣方式就是對二維圖像函數或者是掃描後的圖像信號（一維時間函數）進行等間隔採樣，例如對於5.5MHz帶寬的電視信號，其採樣頻率應等於或大於11MHz。這就要求A/D變換器速率很高。一般這樣高速採樣數據往往先直接存入IC構成的幀存儲器。再由計鐘一機或數字硬體按可能的速度進行運算處理。

　　（2）正交採樣

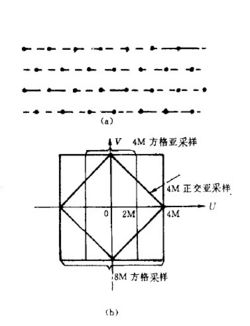
　　所謂正交採樣，就是相鄰行的採樣點交義分佈如圖2（a）。這種採樣方式在某些場合下應用是有效的。例如變化不大的人頭像為主的會議電視圖像，統計計算分析表明，這類圖像頻譜能量絕大部分集中在以原點為中心的菱形區域，而正交採樣的最大不混疊區域也是呈菱形分佈。圖2（b）為方格採樣和正交採樣的最大不混疊範圍。可見4MHz正交採樣和8MHz的方格採樣水平和垂直解析度差不多，只是VU45。方向上稍差些。當然這種採樣方式還要進行對角濾波等處理。

　　（3）縱向採樣

　　某些場合圖像獲取速度很快（如電視攝像機）但後面運算處理器（如微型電腦）的速度跟不上。就可以採用“快掃慢採”的方式，這就是縱向採樣，如圖3（a）所示。對電視信號來講就是每行取一點，每場（或隔場）取一列，那麼兩個採樣點間隔為行周期64us這樣A/D變換器速率只要求32kHz。一幅512*512像素圖像採樣所需時間應為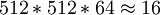s。這種採樣方式對於非實時處理是允許的，可以使器件速度要求下降，成本降低。

　　如果將縱向採樣點送到監視器上，可以在顯示器屏幕看到一根白左向右移動的豎線，如圖3（b）所示。這根線從屏幕最左邊移到最右邊共需16s，也就是全圖採祥時間。

　　二、量化過程

　　量化過程中要討論的第一個問題是量化等級取多少，即通常所講的幾比特量化。從實用觀點出發，因為人們的眼睛對黑白灰度級也只能區別幾十個，因此供人們眼睛觀察的圖像有64個灰度級（即6比特）就夠了。在一些要求嚴格的場合下，或者是電腦要對圖像內容進行定量分析的系統中，往往取25fi個灰度級。在如遙感圖像之類精度要求高的場合，也有取512或1024個灰度級的。若從另外角度出發，由於圖像本身或成像系統存在雜訊，量化級取得太多是沒有必要的，因為如果雜訊幅度大於量化間隔，其輸出誤差就會明顯增加。在應用屏幕顯示時，其灰度鄰近區域邊緣出現“忙亂”現象。假設雜訊是高斯分佈，均值為0，均方誤差為ε²，最佳量化級的選取有兩種辦法:其一是令正確量化的概率大於某一值;其二是量化誤差的方差等於雜訊的方差。總之，量化級數的選取要按圖像內

　　容和應用要求來決定，級數增加，精度高但數據量增加，給後面的傳輸處理識別增加了困難。

　　第二個要討論的問題是採樣幅度值如何分層，一般有兩類:一類是均勻分層即所謂均勻量化;另一類是非均勻分層即所謂非均勻址化。非均勻量化的方式很多，如對供人觀察的圖像按人的視覺特性進行非均勻量化，即對灰度變化緩慢部分細量化，而灰度變化快的部分粗量化，還有針對人的視覺靈敏度呈對數形式的對數非均勻里化。也有從量化誤差角度出發的所謂最佳量化，即使量化誤差最小的非均勻量化。在最佳量化過程中，一般原則是採樣值幅度概率大的細量化，反之粗量化。前幾年國內外都很重視的矢量量化是結合編碼技術的一種量化方式，它不是對每J個樣點值進行量化，而是對樣點序列進行聯合量化，以便提高圖像壓縮比。

　　三、編碼

　　編碼就是對各個量化後的採樣幅值數據用最少的碼字去編成數位輸出，作為數字化的輸出一般是PCM碼。但作為圖像傳輸、存儲或處理過程中的編碼，內容是很多的，如信源編碼日的是儘可能地壓縮圖像數據，以便減少圖像傳輸速率和存儲器容量以及提高運算處理速度。而通道編碼往往是為了防止通道雜訊引起的誤碼儘可能少增加一些比特數。