圖上作業法
出自 MBA智库百科(https://wiki.mbalib.com/)
目錄 |
圖上作業法在運輸圖上求解線性規劃運輸模型的方法。它是在一張運輸交通上通過一定步驟的規劃和計算來完成物資調運計劃的編製工作,以便使物資運行的總噸—公裡數最小可使物資運費降低,並縮短了運輸時間,所以,在一定條件下稱這樣的方案為最優方案。
圖上作業法的步驟[1]
制定一個物資調運方案時:
1、首先要編製物資平衡表(如下圖所示)。
圖1:物資平衡表
在編製物資平衡表時需要做3件事。
(1)出需要調出物資的地點(即發點)及發量。
(2)出需要調進物資的地點(即收點)及收量。
(3)求:總發量=總收量。
2、第二步,根據物資平衡表和收點,發點間的相互位置繪製交通圖。所謂交通圖就是表明收點和發點間的相互位置以及聯結這些點之間的交通線路的簡要地圖。在交通圖上,用圓圈“〇”表示發點,將該發點的發量填入圓圈“〇”內。用方框“□”表示收點,將該收點的收量填入方框“□”內。兩點間的距離,記在交通線路的旁邊。
3、第三步,交通圖繪製好後,即可在其上面進行物資調運,找出初始調運方案(初始基可行解),作物資調運流向圖。
我們用箭頭“→”表示物資調運的方向即稱流向,並規定:流向“→”必須畫在沿著線路前進的右側。把運送物資的數量記在流向“→”的旁邊並加括弧( ),以區別於兩點之間的距離數。
另一方面,為了保持圖面的整潔,流向量最好不要通過收,發點以及交叉路口,如圖1中,(a),(b)是正確的。
圖上作業法的註意事項[1]
在物資運輸中,把某種物資從各發點調到各收點的調運方案是很多的,但我們的目的是找出噸—公裡數是最小的調運方案。這就要註意在調運中不要發生對流運輸和迂迴運輸,因此,我們在制定流向圖時,就要避免它的出現。
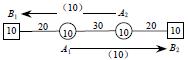
(1)對流:所謂對流就是在一段線路上有同一種物資往返運輸(同一段線路上,兩各方向都有流向),如下圖。
圖2
圖3
將某種物資10噸從A1運往B2,同時又有同樣的物資10噸同時從A2運往B1,於是在A1A2之間就出現了對流現象.如果把流向圖改成圖3,即將A1的10噸運往B1,而將A2的10噸運往B2,就避免了A1A2的對流,從而可以節約運輸量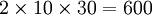 (噸公裡)。
(噸公裡)。
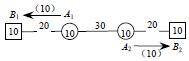
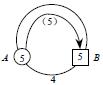
(2)迂迴:當交通圖成圈時,如果流向圖中內圈流向的總長(簡稱內圈長)或外圈流向的總長(簡稱外圈長)超過整個圈長的一半就稱為迂迴運輸。例如某物資流向圖如下圖4所示。
圖4
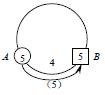
圖5
顯然,它是一個迂迴運輸流向圖,它的內圈長6大於整個圈長的一半5。如果把它改成圖5,就避免了迂迴現象,可節約運輸量 (噸公裡)
理論上可以證明,一個物資調運方案中,如果沒有對流和迂迴運輸,則該方案就是最優調運方案。即運輸量最小的方案。
(噸公裡)
理論上可以證明,一個物資調運方案中,如果沒有對流和迂迴運輸,則該方案就是最優調運方案。即運輸量最小的方案。
從以上討論可以看到,圖上作業法的實質就是在一張交通圖上尋找沒有對流和迂迴的最優流向圖。
為了貫徹以上原則,則須採用逐步逼近法,即我們可以先設法作一個流向圖,然後來檢查它是不是最優的,如果是的話,問題就解決了;如果不是,就把這個流向圖稍微變化一下,這樣的變化稱為調整。調整後的新流向圖所花費的噸公裡比原流向圖的要少一些。然後再檢查新流向圖是不是最優的,如果仍舊不是,就再進行調整,一直到找到最優流向圖為止。
物資運輸的交通圖總共分為兩類:
一類是不成圈的交通圖;
另一類是成圈交通圖。
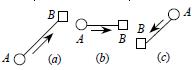








圖形舉例過於簡單 ,應該再引申一兩個複雜的