雙因素方差分析
出自 MBA智库百科(https://wiki.mbalib.com/)
雙因素方差分析法(Two-way analysis of variance)
目錄 |
雙因素方差分析法是一種統計分析方法,這種分析方法可以用來分析兩個因素的不同水平對結果是否有顯著影響,以及兩因素之間是否存在交互效應。一般運用雙因素方差分析法,先對兩個因素的不同水平的組合進行設計試驗,要求每個組合下所得到的樣本的含量都是相同的。
在實際問題的研究中,有時需要考慮兩個因素對實驗結果的影響。例如飲料銷售,除了關心飲料顏色之外,我們還想瞭解銷售地區是否影響銷售量,如果在不同的地區,銷售量存在顯著的差異,就需要分析原因。採用不同的銷售策略, 使該飲料品牌在市場占有率高的地區繼續深入人心,保持領先地位;在市場占有率低的地區,進一步擴大宣傳,讓更多的消費者瞭解、接受該產品。若把飲料的顏色看作影響銷售量的因素A,飲料的銷售地區則是影響因素B。對因素A和因素B同時進行分析,就屬於雙因素方差分析的內容, 雙因素方差分析是對影響因素進行檢驗,究竟是一個因素在起作用,還是兩個因素都起作用,或是兩個因素的影響都不顯著。
雙因素方差分析有兩種類型:
一個是無交互作用的雙因素方差分析,它假定因素A 和因素B的效應之間是相互獨立的,不存在相互關係;
另一個是有交互作用的雙因素方差分析,它假定因素A和因素B的結合會產生出一種新的效應。
例如,若假定不同地區的消費者對某種顏色有與其他地區消費者不同的特殊偏愛,這就是兩個因素結合後產生的新效應,屬於有交互作用的背景;否則,就是無交互作用的背景。有交互作用的雙因素方差分析已超出本書的範圍,這裡介紹無交互作用的雙因素方差分析。
雙因素方差分析的數據結構如下表所示:
| 因素A | 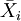
| |||||
|---|---|---|---|---|---|---|
| A1 | A2 | … | Ar | |||
| 因素B | B1 | X11 | X12 | … | X1r | 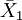
|
| B2 | X21 | X22 | … | X2r | 
| |
| … | … | … | … | … | … | |
| Bk | Xk1 | Xk2 | … | Xkr | 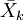
| |
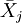 | 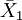 |  | … | 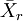 | 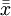
| |
上表,因素A位於列的位置,共有r個水平,\bar{x}_j代表第j種水平的樣本平均數;因素B位於行的位置,共有k個水平,\bar{x}_i代表第i種水平的樣本平均數。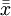 為樣本總平均數,樣本容量
為樣本總平均數,樣本容量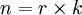 。
。
每一個觀察值Xij看作由A因素的r個水平和B因素的k個水平所組合成的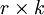 個總體中抽取樣本容量為1的獨立隨機樣本。這
個總體中抽取樣本容量為1的獨立隨機樣本。這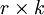 個總體的每一個總體均服從正態分佈,且有相同的方差。這是進行雙因素方差分析的假定條件。
個總體的每一個總體均服從正態分佈,且有相同的方差。這是進行雙因素方差分析的假定條件。








看不懂