利潤方程式
出自 MBA智库百科(https://wiki.mbalib.com/)
目錄 |
利潤方程式是本量利分析基礎,它體現著營業收入總額、成本總額和營業利潤之間的關係。
利潤方程式的計算方法[1]
即:
[[營業利潤]]=營業收入總額-成本總額
用公式表示即
π=TR-TC
營業收入總額與成本總額兩者都要受產出數量變化的影響。營業收入總額(TR)等於每單位平均售價(P)乘上產出的單位數(X):TR=P·X。成本總額(TC)可以劃分為不隨產出水平的變化而變化的固定部分,以及隨產出變化而變化的變動部分。固定部分是由每期固定成本總額(F)所構成,而變動部分系每單位平均變動成本(V)乘上產出數量(X)之積,所以,成本函數是:TC=V·X+F。將收入函數與成本函數代入利潤方程式,得出一種更為有用的形式如下:
π=TR-TC
π=P·X-(V·X+F)
合併同類項,得
π=(P-V)·X-F
或:
π+F=(P-V)·X
上列利潤方程式中所列示的(P-V)就是單位產品邊際貢獻,(P-V)·X為邊際貢獻總額,用以:(1)抵償固定成本(F);(2)提供營業利潤π)。
註意,V是單位製造成本和單位推銷及管理成本之和;F是該期固定製造成本、固定推銷成本以及固定管理成本總額之和,X指該期生產和銷售的單位數(假定生產與銷售數量相同,不考慮期初、期末存貨的影響)。
利潤方程式的實例分析[1]
例如:某公司經營汽車業務,在3月份,該公司購入20輛汽車,並以每輛45,000元售,出,下麵是每輛汽車的平均變動成本數據:
| 每輛汽車的成本 | 36900 |
| 準備成本 | 300 |
| 銷售佣金 | 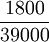 元 元
|
| 每輛平均變動成本 |
該公司經營的月平均固定成本為90000.使用利潤方程式計算,該月份的經營成果如下:
π=(P-V)·X-F=(45000-39000)×20-90000=30000元
上面的營業利潤30000元是用代數方法計算求得的,也可以用對該公司該月的成本流轉和收益表進行分析的辦法來計算:
- 某公司收益表 2月份
| 銷售(20輛@45000) | 900000 |
| 變動銷貨成本 | 744000 |
| 變動推銷成本 | 36000 |
| 邊際貢獻 | 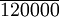
|
| 固定成本 | 90000 |
| 營業利潤 | 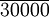 元 元
|







