幾何級數增長

出自 MBA智库百科(https://wiki.mbalib.com/)

幾何級數增長(geometric growth)

　　幾何級數增長就是成倍數增長。類似與通常說的“翻番”——2、4、8、16、32、64、128等等，或者3、9、27、81等等。在幾何上，面積與邊長的關係是乘積的函數關係。因此也將成倍增長稱為“幾何級數增長”。

　　在具體討論現實的種群在有限的環境中增長過程以前，首先介紹一個理想的種群在無限的環境中增長的模型。假定有一種一年只有一個繁殖季、壽命只有一年的動物，那麼其世代是不重疊的。例如，棲居於草原季節性小水坑中的水生昆蟲，每年雌蟲產一次卵，卵孵化長成幼蟲，蛹在泥中度過乾旱季節。到第二年，蛹才變為成蟲，交配、產卵。因此，世代是不重疊的，種群增長是不連續的。假定這些水坑是彼此隔離的，即種群沒有遷入和遷出。

　　1．模型的假設和概念結構

　　在這個最簡單的單種種群增長模型的概念結構里，包含有下列四個假設：①種群增長是無界的，即設種群在無限的環境中增長，沒有受資源、空間等條件的限制；②世代不相重疊。增長是不連續的，或稱離散的；③種群沒有遷入和遷出；④沒有年齡結構。

　　2．數學模型

　　式中：N為種群大小，t為時間，λ為種群的周限增長率。

　　3．模型的生物學含義

　　下麵我們對這個模型的生物學含義作進一步解釋。

　　如果種群在無限環境下以這個速率年復一年地增長，即

　　N₀ = 10

　　……

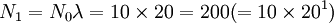
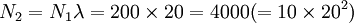
　　N_{t + 1} = N_tλ或N_t = N₀λ'

　　λ在此是表示種群以每年(或其他時間單位)為前1年20倍的速率而增長的增長率，稱為周限增長率。這種增長形式稱為幾何級數式增長或指數式增長。

　　它具有直線方程式y=a+bx的形式。因此，以lgN_t與t作圖，就能得到一條直線，其中lgN₀是直線的截距，lgλ是直線的斜率。

　　4．模型的參數λ

　　周限增長率λ是種群增長模型中有用的量，如果λ = N_{t + 1} / N_t = 1，表示種群數量在t時和t+1時相等，種群穩定。從理論上講，λ可以有下麵四種情況，它在種群增長中的含義是：

　　λ>1，種群上升；

　　λ=1，種群穩定；

　　0<λ<1，種群下降；

　　λ=0，雌體沒有繁殖，種群在一代中滅亡。