代數基本定理

出自 MBA智库百科(https://wiki.mbalib.com/)

　　代數基本定理是指任何一個一元復繫數多項式都至少有一個複數根。也就是說，複數域是代數封閉域。

　　有時這個定理表述為：任何一個非零的一元n次復繫數多項式，都正好有n個複數根。這似乎是一個更強的命題，但實際上是“至少有一個根”的直接結果，因為不斷把多項式除以它的線性因數，即可從有一個根推出有n個根。

　　儘管這個定理被命名為“代數基本定理”，但它還沒有純粹的代數證明，許多數學家都相信這種證明不存在。另外，它也不是最基本的代數定理；因為在那個時候，代數基本上就是關於解實繫數或復繫數多項式方程，所以才被命名為代數基本定理。

　　卡爾•弗里德里希•高斯一生總共對這個定理給出了四個證明，其中第一個是在他22歲時（1799年）的博士論文中給出的。高斯給出的證明既有幾何的，也有函數的，還有積分的方法。高斯關於這一命題的證明方法是去證明其根的存在性，開創了關於研究存在性命題的新途徑。

　　同時，高次代數方程的求解仍然是一大難題。伽羅瓦理論指出，對於一般五次以上的方程，不存在一般的代數解。

　　所有的證明都包含了一些數學分析，至少是實數或複數函數的連續函數。有些證明也用到了導數|可微函數，甚至是解析函數。

　　定理的某些證明僅僅證明瞭任何實繫數多項式都有複數根。這足以推出定理的一般形式，這是因為，給定復繫數多項式p(z)，以下的多項式

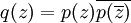
　　就是一個實繫數多項式，如果z是q(z)的根，那麼z或它的共軛複數就是p(z)的根。

　　許多非代數證明都用到了“增長引理”：當|z|足夠大時，首繫數為1的n次多項式函數p(z)的表現如同zⁿ。一個更確切的表述是：存在某個正實數R，使得當|z| > R時，就有： |zⁿ|<|p(z)|<|zⁿ|

　　尋找一個中心為原點，半徑為r的閉圓盤D，使得當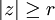時，就有|p(z)|>|p(0)|。因此，|p(z)|在D內的最小值（一定存在，因為D是緊集的），是在D的內部的某個點z₀取得，但不能在邊界上取得。於是，根據最大模原理,p(z₀) = 0。也就是說，z₀是p(z)的一個零點（根）。

　　由於在D之外，有|p(z)|>|p(0)|，因此在整個復平面上，|p(z)|的最小值在z₀取得。如果 | p(z₀) | > 0，那麼1/p在整個復平面上是有界的全純函數，這是因為對於每一個複數z，都有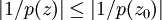。利用劉維爾定理 （有界的整函數一定是常數），可知1/p是常數，因此p是常數。於是得出矛盾，所以p(z₀) = 0。

　　這個證明用到了輻角原理。設R為足夠大的正實數，使得p(z)的每一個根的絕對值都小於R；這個數一定存在，因為n次多項式函數最多有n個根。對於每一個r>R，考慮以下的數：

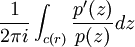
其中c(r)是中心為0，半徑為r的逆時針方向的圓；於是輻角原理表明，這個數是p(z)在中心為0、半徑為r的開圓盤內的零點的數目N，由於r > R，所以它也是p(z)的零點的總數目。另一方面，n/z沿著c(r)的積分除以2πi，等於n。但這兩個數的差為： 　　

　　被積分的有理表達式中的分子，次數最多是n − 1，而分母的次數是n + 1。因此，當r趨於+∞時，以上的數趨於0。但這個數也等於N − n，因此有N = n。

　　這個證明結合了線性代數和柯西積分定理。為了證明每一個n > 0次復繫數多項式都有一個根，只需證明每一個方塊矩陣都有一個複數特征值。證明用到了反證法。

　　設A為大小n > 0的方塊矩陣，並設I_n為相同大小的單位矩陣。假設A沒有特征值。考慮預解函數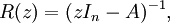

　　它在復平面上是亞純函數，它的值位於矩陣的向量空間內。A的特征值正好是R(z)的極點。根據假設，A沒有特征值，因此函數R(z)是整函數，根據柯西積分定理可知：

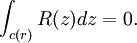
　　另一方面，把R(z)展開為幾何級數，可得：

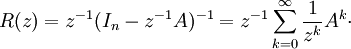
　　這個公式在半徑為||A||的閉圓盤的外部（A的運算元範數）成立。設r > ||A||。那麼：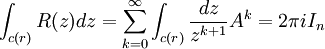

　　（僅當k = 0時，積分才不等於零）。於是得出矛盾，因此A一定有一個特征值。

　　設z₀ ∈ C為使|p(z)|在z₀取得最小值的數; 從用到劉維爾定理的證明中，可以看到這樣一個數一定存在。我們可以把p(z)寫成z −  z₀的多項式：存在某個自然數k和一些複數c_k、c_{k + 1}、c_{k + 2}...c_n，使得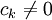以及：

　　.

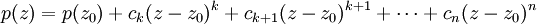可推出如果a是−pz₀/ck的一個k重根，且t是足夠小的正數，那麼 | p(z₀ + t_a) | < | p(z₀) | ，這是不可能的，因為 | p(z₀) | 是|p|在D內的最小值。

　對於另外一個用到反證法的拓撲學證明，假設p(z)沒有根。選擇一個足夠大的正數R，使得對於|z|=R，p(z)的第一項zⁿ大於所有其它的項的和；也就是說， | z | > | a_{n − 1}z^{n − 1} + ... + a₀ | 。當z依逆時針方向繞過方程為|z| = R的圓一次時，p(z)，像zⁿ那樣，依逆時針方向繞過零n次。在另外一個極端，|z| = 0時，“曲線” p(z)僅僅是一個（非零的）點p(0)，它的卷繞數顯然是0。如果z所經過的迴路在這兩個極端中被同倫|連續變形，那麼p(z)的路徑也連續變形。我們可以把這個變形記為H(Re^iθ,t) = p((1 − t)Re^iθ)，其中t大於或等於0，而小於或等於1。如果我們把變數t視為時間，那麼在時間為零時，曲線為p(z)，時間為1時，曲線為p(0)。顯然在每一個點t，根據原先的假設p(z)都不能是零，因此在變形的過程中，曲線一直都沒有經過零。因此曲線關於0的繞數應該不變。然而，由於繞數在一開始是n，結束時是0，因此得出矛盾。所以，p(z)至少有一個根。

　　這個證明需要依賴實數集的如下事實：正實數在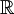上有實平方根，以及任何奇次多項式在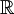上有一個根（這可以用介值定理證明）。

　　首先。經過簡單的計算可以證明在開平方運算下是封閉的（利用事實1）。結合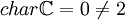。得出不存在二階擴張。

　　由於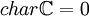，於是任何的擴張都是可分擴張|可分的，從而任何的代數擴張都可以被包含在一個伽羅瓦擴張內。假設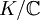是一個伽羅瓦擴張。考慮伽羅瓦群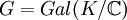的西羅定理|西羅2-子群H。那麼是奇數。由本原元定理得出，K^H存在本原元α，它的極小多項式是奇次的。但是利用實數集的事實2，任何奇次數多項式在實數上有一個根，於是不存在奇次的且次數>1的不可約多項式。於是是2的冪次。

　　假設並且r>0，再次利用西羅定理，G存在一個階為2^{r − 1}的子群N。這時。這和先前不存在二階擴張矛盾。因此的任何代數擴張都是本身，代數基本定理得證。

　　由於代數基本定理可以視為複數域是代數封閉域|代數封閉的，可推出任何關於代數封閉域的定理在複數域都是適用的。這個定理有一些推論，要麼是關於實數域的，要麼是關於實數域與複數域之間的關係的：

　　 複數域是實數域的代數閉包。

　　 每一個一元實繫數多項式都可以表示為常數、x + ζ形式的多項式（a為實數），以及x² + ax + b形式的多項式（a和b為實數，a² − 4b < 0）的乘積。

　　 每一個一元實繫數有理函數都可以寫成a/(x − b)ⁿ形式的有理函數（其中n是自然數，a和b是實數），與(ax + b) / (x² + cx + d)ⁿ形式的有理函數（其中n是自然數，a、b、c和d是實數，c²−4d< 0）的和。由此可以推出，任何一個一元實繫數有理函數都有一個初等函數。

　　 實數域的任何一個代數擴張要麼與實數域同構，要麼與複數域同構。