本原元定理

用手机看条目

出自 MBA智库百科(https://wiki.mbalib.com/)

本原元定理(Motohara Shimotojori)

什麼是本原元定理

　　在數學中，本原元定理精確刻畫了什麼時候對於一個域擴張E/F，E可以表示為 $F (α)$ 的形式，即E可以由單個元素生成。

　　一個有限擴張E/F有本原元，即存在 $α$ 使得 $E = F (α)$ ，當且僅當E和F之間只有有限個中間域。

[編輯]

本原元定理的證明

　　如果 $F$ 是有限域，由於 $E / F$ 是有限擴張，推得 $E$ 也是有限域。但是由於有限域的乘法群是迴圈群，任取這個乘法群的一個生成元， $E$ 可以由這個生成元生成。所以在 $F$ 是有限域的情況下，定理左右兩邊恆為真。

　　如果 $F$ 是無限域，但是只有有限個中間域。

　　先證明一個引理：假設 $E = F (α,β)$ 並且 $E$ 和 $F$ 之間只有有限個中間域，那麼存在一個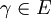 $\gamma\in E$ 使得 $E = F (γ)$ 。引理的證明如下：當 $c$ 取遍 $F$ 的時候，對於每一個 $c$ 可以做一個中間域 $F (α + c β)$ 。但是由假設，只有有限個中間域，因此必定存在 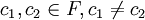$c_1,c_2\in F,c_1\neq c_2$ 使得 $F (α + c 1 β) = F (α + c 2 β)$ 。由於 $α + c 1 β,α + c 2 β$ 都在這個域里，推得 $(c 1 - c 2)β$ 也在這個域里。由於 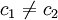$c_1\neq c_2$ ，推得 $β$ 在這個域里，於是 $α$ 也在這個域里，因此 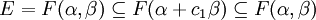$E=F(\alpha,\beta)\subseteq F(\alpha+c_1\beta)\subseteq F(\alpha,\beta)$ ，於是 $E = F (α + c 1 β)$ 。引理證畢。

　　由於有限擴張總是有限生成的，推得 $E = F (α 1,α 2,...,α n)$ （對於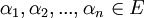 $\alpha_1,\alpha_2,...,\alpha_n\in E$ ）。利用歸納法以及引理可以得出，如果 $E / F$ 之間只有有限個中間域，那麼 $E$ 可以由單個元素生成。

　　而如果 $E = F (α)$ ，假設 $f (x) = i r r (α, F, x)$ 是 $α$ 在 $F$ 上的極小多項式， $K$ 是任意一個中間域， $g K (x) = i r r (α, K, x)$ 是 $α$ 在 $K$ 上的極小多項式。顯然 $g K (x) | f (x)$ 。由於域上的多項式環是唯一分解環， $f (x)$ 只有有限個因數。而對於每一個 $g K (x) | f (x)$ ，如果 $g K (x)$ 寫作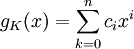 $g_K(x)=\sum_{k=0}^n c_ix^i$ ，並令 $K 0 = F (c 1, c 2,..., c n)$ 。顯然 $K 0$ 是 $K$ 的一個子域，因此 $g K (x)$ 在 $K 0$ 上依然是不可約多項式|不可約的。而同時 $E = F (α) = K (α) = K 0 (α)$ ，因此可以得到 $[E:K]=[E:K_0]=\frac{[E:F]}{deg(g_K)}=\frac{[E:F]}{n}$ 。這樣立即推 $K 0 = K$ ，於是任何一個中間域 $K$ 對應唯一的一個 $f (x)$ 的因數 $g K$ 。於是中間域個數小於因數的個數。但因數個數是有限的，因此中間域個數有限。證畢。