烏鴉悖論

出自 MBA智库百科(https://wiki.mbalib.com/)

烏鴉悖論，也叫做亨佩爾的烏鴉、亨佩爾悖論、確證悖論、亨普爾悖論，是二十世紀四十年代德國邏輯學家卡爾·古斯塔夫·亨佩爾（Carl Gustav Hempel）為了說明歸納法違反直覺而提出的一個悖論。

　　幾千年以來，無數人觀察了許多事務，比如地心引力法則，人們趨於相信其極可能是真理。這種類型的推理可以總結成“歸納法原理”：

　　如果實例X 被觀察到和論斷 T 相符合，那麼論斷 T 正確的概率增加。

　　亨佩爾給出了歸納法原理的一個例子：“所有烏鴉都是黑色的”論斷。我們可以出去觀察成千上萬隻烏鴉，然後發現他們都是黑的。在每一次觀察之後，我們對“所有烏鴉都是黑的”的信任度會逐漸提高。歸納法原理在這裡看起來合理的。^[1]

　　現在問題出現了。“所有烏鴉都是黑的” 的論斷在邏輯上和“所有不是黑的東西不是烏鴉”等價。如果我們觀察到一隻紅蘋果，它不是黑的，也不是烏鴉，那麼這次觀察必會增加我們對“所有不是黑的東西不是烏鴉”的信任度，因此更加確信“所有的烏鴉都是黑的”！這個問題被總結成：

• 我從未見過紫牛，I never saw a purple cow
• 但若我見到一頭，But if I were to see one
• 烏鴉皆黑的概率，Would the probability ravens are black
• 更加可能是一麽？Have a better chance to be one?

　　（改寫自吉利特·伯吉斯（Gelett Burgess）的詩）

　　烏鴉悖論又叫做確證悖論，是一個有關科學中的普遍性見解的確證或支持的難題。

　　為正確理解這個難題，首先需要明白三個概念，即證明、確證和否證。

　　我們所說的證明具有最終的含義。證明有兩種情況，一種是理論證明，一種是經驗證明。

　　一個特殊的結論如果能夠從一個尚未發現問題的普遍性見解中推導出來，我們就說這個特殊的結論得到了理論證明。

　　比如，“張三必有一死”這個結論就可以這樣來證明：凡人皆有一死，而張三是人，所以張三必有一死。從這裡可以看出，理論證明的一個重要條件就是，證明中所利用的普遍性見解必須正確。普遍性見解的正確性不能靠理論證明，而要靠經驗證明。

　　一個普遍性的結論如果其中所能包括的所有特殊情況都被人們正確無誤地一一觀察到，我們就說這個普遍性的結論得到了經驗證明。

　　普遍性的結論包括的特殊情況無窮多，所以經驗證明往往是不可能的。上面的例子中，“凡人必有一死”這個見解， 就要靠觀察以前、現在和將來所有的人是否都有一死來證明。

　　根據一個普通性的見解預見一個新穎的特殊情況，如果確實觀察到這個特殊的情況，那麼，這個觀察就成為一個證據而支持這個普遍性見解，於是我們就說這個普遍性的見解得到了確證。相反，如果觀察到的情況不像所預見 的那樣，我們就說這個普遍性的見解被否證。

　　我們要介紹的亨普爾悖論就是一個有關科學中的普遍性見解的確證或支持的難題，所以它又叫做“確證悖論”。

　　至此，人們關於確證或支持的看法有4個，即：

　　(1)觀察到一隻黑渡鴉，將支持“凡渡鴉皆黑”的見解；

　　(2)觀察到一個非黑色而又並非是渡鴉的東西，會支持“非黑者皆非渡鴉”的見解；

　　(3)“凡渡鴉皆黑”和“非黑者皆非渡鴉”是兩個相當的見解，因此同一個觀察結果對它們要麼都支持，要麼都不支持，就是說，不會出現同一個觀察結果只支持這兩個見解中的一個而不支持這其中的另一個的情況；

　　(4)觀察到一隻白鞋，不會支持“凡渡鴉皆黑”的見解。

　　1945年，美國科學哲學家卡爾.亨普爾發現，這4個看法放在—起不兼容。

　　比如我們觀察到—只白鞋，那麼根據(2)，因為白鞋是一件非黑而且並非渡鴉的東西，所以這個觀察就會支持“非黑者皆非渡鴉”的見解。根據(3)，這個觀察也會支持“凡渡鴉皆黑”的見解，這個結論正好與(4)完全相反。這樣就出現了矛盾。由於這個問題是以渡鴉為例提出來的，所以又稱為“渡鴉悖論”。

　　確證在科學中起著非常重要的作用，是科學哲學家們十分重視的問題。半個世紀以來，人們圍繞亨普爾悖論已經發表了大量的論文，提出了各種各樣的見解，但是迄今卻沒有一個公認的解決方案出現。

　　解決它和直覺的衝突，哲學家們提出了一些方法。美國邏輯學家納爾遜·古德曼（Nelson Goodman）建議對我們的推理添加一些限制，比如永遠不要考慮支持論斷“所有P滿足Q”且同時也支持“沒有P滿足Q” 的實例。

　　其他一些哲學家質疑“等價原理”。也許紅蘋果能夠增加我們對論斷“所有不是黑的東西不是烏鴉”的信任度，而不增加我們對 “所有烏鴉都是黑色的”信任。這個提議受到質疑，因為你不能對等價的兩個命題有不同的信任度，如果你知道他們都是真的或都是假的。

　　古德曼，以及其後的威拉德·馮·奧曼·蒯因，使用術語“projectible predicate”來描述這些類似於“烏鴉”和“黑色”的命題, 所有這類命題是支持歸納推理法的；而“非projectible predicate”則為與只相反的後者, 如“非黑”和“非烏鴉”這些命題並不支持歸納推理法。蒯因還提出一個需要證實的猜想：如果任何命題是projectible的；在無限物件組成的全集中，一個projectible的命題的補集永遠是非projectible的。

　　這樣一來，雖然“所有烏鴉都是黑的”和“所有不是黑的東西都不是烏鴉”這兩個命題所擁有的信任度必須相等，但只有“黑色的烏鴉”才能同時增加兩者的信任度，而“非黑色的非烏鴉”並不增加任何一個命題的信任度。

　　還有些哲學家認為其實這個命題是完全正確的，出錯的是我們自己的邏輯。其實觀察到一個紅色的蘋果確實會增加烏鴉都是黑色的可能性！這就相當於：如果有人把宇宙中所有不是黑的物體都給你看，而你發現所有的物體都不是烏鴉，那你就完全可以斷定所有烏鴉都是黑的了。這個“悖論”看上去荒謬只是因為宇宙中 “不是黑的”物體遠遠多於“烏鴉”，所以發現一個“不是黑的”物體只增加了極其微小的對於“烏鴉都是黑的”的信任度，而相對而言，每發現一隻黑的烏鴉就是一個有力的證據了。

　　此外，火雞思維主張科學始於觀察，觀察提供科學知識能夠賴以確立的可靠基礎，而科學知識是用歸納法從有限的觀察陳述中推導出來的，所以說這種歸納法得出的結論未必是正確的，甚至可能是非常可笑的。所以烏鴉悖論的手段和方法，正好與火雞問題相悖，這就是一個對立的哲學命題。

　　除了以上的陳述以外，「歸納法原理」還有另一種形式，就是貝葉斯推理。

　　設 X 為支持論斷 T 的一個實例, 而 I 表示我們所有的已知信息。

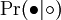　　 表示論斷 T 成立的幾率，已知 X 和 I 都是成立的，可以推得，

　　這裡 Pr(T | I) 表示在只有 I 是已知成立的情況下，T 成立的幾率；Pr(X | TI) 表示在 T 和 I 都已知成立的情況下，X 成立的幾率；而 Pr(X | I) 表示在只有 I 是已知成立的情況下，X 成立的幾率.

　　利用這個原理，這個悖論就不會出現了。如果有人隨機選一個蘋果，那麼他看到一個紅蘋果的幾率和「烏鴉」的顏色是完全沒有關係的。這時分子等於分母，所以分數等於1，所以以上討論的幾率不會改變。所以看見一隻紅色的蘋果不會增加人們對「烏鴉都是黑色的」的信任度。

　　而如果那人是隨叫隨到選擇一個非黑的物件，那個物件正好是一個紅的蘋果，那麼我們對得到一個分子大於分母的，幾乎等於一的假分數。所以在這個情況下，看見一隻紅蘋果確實會極微小地增加我們對「烏鴉都是黑色的」的信任度。

　　其實，隨著一個人看到的不是黑色的東西的增加（併發現其中沒有烏鴉），「烏鴉都是黑色的」的幾率會趨向於1。

• 貝葉斯定理
• 貝葉斯推理
• 火雞思維