效用函数
出自 MBA智库百科(https://wiki.mbalib.com/)
效用函数(Utility Function / Effectiveness Function / Utility Function Used)
目录 |
"效用函数" 在工具书中的解释
表示消费者在消费中所获得的效用与所消费的商品组合之间数量关系的函数。它被用以衡量消费者从消费既定的商品组合中所获得满足的程度。运用无差异曲线只能分析两种商品的组合,而运用效用函数则能分析更多种商品的组合。其表达式是:U=U(x, y, z, …)式中 x, y, z分别代表消费者所拥有或消费的各种商品的数量。
"效用函数" 在学术文献中的解释
1、效用函数的定义是:设f是定义在消费集合X上的偏好关系,如果对于X中任何的x,y,xfy当且仅当u(x)u(y),则称函数u:XnR+R是表示偏好关系f的效用函数。[1]
2、F(X)称为效用函数.加权P范数法的关键是权系数的确定.有2种基本的方法,一是老学习法[1,2],该方法依据目标函数的相对重要性来选取权系数。[2]
3、一个人的效用应是财富x的函数,这个函数称为效用函数,从理论上来讲,它可以通过一系列心理测试来逼近得到每个人的效用函数.不同的决策者应有不同的效用函数.首先我们寻求效用函数所满足的性质或某些特殊类效用函数所满足的性质。[3]
4、这是一种理论假设,他们运用的数学函数式所建立的模型称为“效用函数”.按照这类模型,人都能被假设成为可以决定在每一种可能的时间分配中产生一定的利益水平,并且追求利益最大化的选择。[4]
T——第i种运输方式的出行时间;
C——第i种运输方式的运输费用。[5]
6、为了对控制做出评价,需要一套函数作为评价指标: 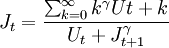 其中Ut = U[Rt,At,t]用以对每步控制进行评价,称为效用函数.J(t)函数表示了从此刻开始的每步效用函数值的累积,称为费用函数。[5]
其中Ut = U[Rt,At,t]用以对每步控制进行评价,称为效用函数.J(t)函数表示了从此刻开始的每步效用函数值的累积,称为费用函数。[5]
在现代消费者理论中,以商品价格向量P、消费束(商品数量向量)X、和消费者预算约束m三者为自变量的效用函数形式有两类:一类是仅以消费束X为自变量的“直接效用函数”U(X);另一类是以商品价格向量P和消费者预算约束m两者为自变量的“间接效用函数”v(P,m)。
直接效用函数U(X)的思想是:只要消费者购买(消费)各种商品的数量一定(而不管其他相关的经济变量(如价格向量P)如何置定或变动),消费者的偏好或效用大小便唯一地确定。即,确定的消费束X对应确定的效用函数值U(X)。
间接效用函数v(P,m)是建立在仅以消费束X为自变量的直接效用函数U(X)的基础之上的。其思路是:只要消费者面临的商品价格向量P和消费者预算约束m两者一定,消费者在PX=m约束下,最大化其直接效用函数U(X)的值,此时的最大U(X)值即是间接效用函数v(P,m)的函数值。需要特别指出的是,消费者面临的商品价格向量P和消费者预算约束m两者确定,消费者最大化其效用水平的购买消费束X并不要求唯一确定(虽然大多数时候是唯一确定的),但这些不同的向量X所对应的直接效用函数U(X)的值却必须是唯一的“最大值”。
现代西方经济学关于效用函数与商品价格向量P、消费束(商品数量向量)X、和消费者预算约束m等其他经济变量的关系,被认定为:效用函数值的大小实际上被消费者本人的消费束X唯一地确定;除消费束X之外的其他变量(如P和m)对消费者效用水平的影响,只能通过影响X间接地决定或影响效用水平。即只要消费者购买(或消费)各种商品的数量一定(而不管其他相关的经济变量如价格向量P如何置定或变动),其偏好或效用大小便唯一地确定。然而,实际情形并非如此。
效用函数的存在性,用数学式表示了效用函数的2个特征:效用是随着单个商品数量递增而增长的,且单个商品的边际效用是递减的同时,得出了对于效用函数,商品组合X和商品组合Y产生的效用之和大于商品组合X+Y产生的效用.
西方经济学效用函数的存在性定理[6]:假定消费者偏好具有完备性、自返性、传递性、连续性和强单调性,那么,存在着一个能代表该偏好的连续效用函数。
在上述假设下,西方经济学首先构造一个由所有商品的1个单位所组成的单位消费束e(e是每个分量均为1的n维实数空间Rn中的向量),然后将所有的消费束与这个单位消费束进行比较,“证明”这些所有的消费束都分别与这个单位消费束的某一个倍数是无差异的,从而可以用这个倍数来表示效用,即效用函数是存在的。
但是,西方经济学对效用函数的存在性的证明,是一种自我循环的论证。这是因为,效用函数存在性定理的那些假设条件,不是基于事实,而是基于数学证明的需要。而要满足这些假设条件,就必须事先要求效用函数的存在。事实上,如果没有效用函数的事先存在,消费者是不可能对数百万种商品的各种数量的无穷组合进行满足完备性、传递性和连续性的偏好判断的。而这正是在心理实验中发现那些事先没有设定效用函数的人们的选择缺乏传递性的根本原因。
从而西方经济学所证明的是这样一个定理:假定消费者偏好是用一个能够被数学证明其存在性的连续效用函数来代表的,那么就可以证明存在这样一个能代表该偏好的连续效用函数。
进一步地,上述存在性定理所“证明”的效用函数是连续性的,从而是基数效用,而不是非连续的序数效用。也就是说,序数效用的存在性并没有得到任何证明。而基数效用的最大问题是如何确定“效用单位”。对于一个“效用单位”到底是多少的问题,西方经济学始终没有回答。实际上,从西方经济学关于效用函数存在性的“证明”过程来看,西方经济学实际上隐含地将一个单位消费束即所有商品各消费一个单位所带来的消费效用作为一个效用单位。但是,富人是不会去吃穷人的“珍珠翡翠白玉汤”的。这种汤带给穷人的效用为正,而带给富人的效用为负。从而,穷人和富人有不同的消费集,也就有了不同的单位消费束。那么应当按哪一个消费束来算呢?尤其是对于那些财富的数量每天在变动的人,比如今天还是白领、明天就失业成为穷人的人。
还有一个问题就是一个商品的消费单位如何计算?比如,对于水和粮食,如果都用吨来计算,那么我们可以设想这样一个情形:假定对某个消费者来说,3吨水和0.1吨粮食是其在某个沙漠地区生存一段时间所必需的。用x=(3,0.1)来表示此消费束。也就是说,我们在这里只考虑一个简单的二维消费空间,其中的一维代表水,另一维代表粮食。于是,按照西方经济学关于效用函数存在性的证明,存在某个0.1<t<3,使得t(1,1)即(t,t)与(3,0.1)是无差异的,也就是说消费t吨水和t吨粮食与消费3吨水和0.1吨粮食是无差异的。然而,在沙漠里,失去的(3-t)吨水是不可以用增加的(t-0.1)吨粮食来代替的[4]。当然,西方经济学可以将3吨水和0.1吨粮食分别视为一个单位的水和一个单位的粮食,以便维持消费所需的正常比例。但是,这样一来,各个商品的消费单位的认定就过于随意了,而这种不同单位的转换未必能保证存在性证明所需要的单调性,从而可能破坏效用的序数性质。
实际上,如果不能确定一个单位消费束中的所有商品的一个消费单位,那么效用函数的存在性“证明”也就缺乏现实基础。此外,我们注意到两个单位消费束即2e的效用恰好是一个单位消费束e效用的两倍,ne的效用恰好是e的效用的n倍。也就是说,如果将一单位消费束看作一个综合商品,那么该综合商品的边际效用是恒定的,与西方经济学的边际效用递减相矛盾。
更进一步地,西方经济学仅仅“证明”了效用函数的存在性,并没有求出具体的效用函数。但西方经济学却因此获得了可以任意设定效用函数的权力。例如,我们可以从西方经济学教材中看到如下效用函数形式
u(x,y) = xayb
其中,x,y分别是两个商品的消费量,U(x,y)是消费这样一个消费束给消费者带来的效用,a>0,b>0。
上述并未被数学证实的效用函数形式,存在这样一个问题:考虑一个又饥又渴的人。设x,y分别代表水和面包的消费量,则上述效用函数意味着,给这个消费者一粒面包屑和无穷多的水,或者给这个消费者一滴水和无穷多的面包,都可以让该消费者得到无穷大的效用。但是,在现实生活中,上述两个消费束带给这个消费者的无穷大效用还不如两杯水加两个面包带给他的有限效用,后者更能适合他的需要。这个例子表明,西方经济学不仅滥用了所谓效用函数的存在性,甚至无法给出一个不与人们的现实感受相冲突的具体的效用函数形式。
案例一:效用函数在金融学中的应用[7]
1952年,Markowitz发表《投资组合选择》,揭开了金融数学的发展。半个世纪来,现代金融理论经历了由简单的定量分析到系统化,再到工程化的过程。这个过程中,效用函数成为研究金融理论的强有力工具。一些学者利用效用函数对Markowitz的均值一方差组合模型进行改进,形成了一些很实用的模型,比如金融学中常用的无差异曲线。有的学者考虑到投资者对收益与风险的偏好,建立了基于投资者的指数型效用函数和幂函数等,本文将讨论效用函数的这两种形式,并利用它们分析效用函数在保险业中的应用。
一、效用函数的幂函数形式
(1)对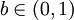 ,定义
,定义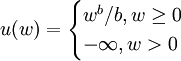
(2)对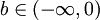 ,定义
,定义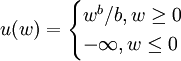
(3)对b=0,定义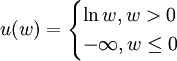
上述(3)中的形式实际上是因为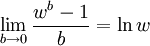
假定ζ > 0是一个有界的随机变量,对上述3种形式,当w>0时,μ(w)都是严格凹函数,利用詹森不等式E(g(ζ)) < g(E(ζ))分别得到:
E(μ(ζ)) = E(ζb / b) < E(ζb) / b,
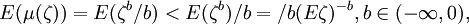 和E(μ(ζ)) = E(lnζ) < ln(Eζ),
和E(μ(ζ)) = E(lnζ) < ln(Eζ),
由此可见,此处预期效用最大化等同于 最大化,这就把问题转化为数学问题。在投资分析中,利用效用函数的幂函数形式能够很方便的解决一些问题。
二、效用函数的指数函数形式
(1)对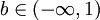 ,定义
,定义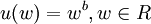 ;
;
(2)对b=0,定义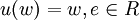
假定ζ > 0是一个有界的随机变量,利用泰勒公式展开式,对(1)有:
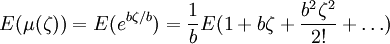
由上式可知,预期效用最大化等同于E(ζ)最大化且Varζ最小化及回报最大化兼顾风险最小化。因此风险与回报问题可以近似于效用函数的最优化问题。
如果 还服从正态分布N(μ,σ2)即满足E(ζ) = μ,Varζ = σ2。当货币收入效用函数具有形式(1)时,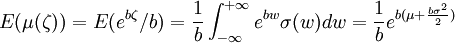 ,其中
,其中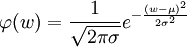 为正态分布密度函数。注意到E(μ(ζ))是递增的,因此如果是在某一单调变换下,预期效用函数E(μ(ζ))可变换为效用函数
为正态分布密度函数。注意到E(μ(ζ))是递增的,因此如果是在某一单调变换下,预期效用函数E(μ(ζ))可变换为效用函数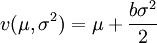 ,这两个函数表示了同一偏好关系。因为v只和均值和方差有关,对风险行为作出回报与风险的评价要方便。
,这两个函数表示了同一偏好关系。因为v只和均值和方差有关,对风险行为作出回报与风险的评价要方便。
三、购买保险与效用函数的形式
假定某人有初始财富收入为W(>0)元,且在一年后因意外原因会损失x(>0)元的概率为P,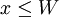 ;而保持初始财富W的概率为1-P,则他在一年后的预期收入为:
;而保持初始财富W的概率为1-P,则他在一年后的预期收入为:
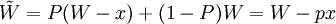 ,
,
此人面临购买保险与不购买保险2种经验选择。
假定保险公司为人们提供保险并不想从个别人身上赚钱,也就是说,保险公司向个人销售保险的预期收入为零(后面还讨论保险公司的经营情况)。用π = RP(ζ)表示保险费,显然0<π<x。如果意外事件发生,他将从保险公司得到x元的赔偿。因此,保险公司销售x元保险的预期收入为:p(π − x) + (1 − p)π = π − px。
在保险公司向个人销售保险的预期收入为零的假设下,容易得到:π = px,即保险费就等于个人可能的损失与意外事件发生概率的乘积。
假设此人愿意支付保险费,并仍假定为п,则当意外事件发生时,他会得到 元保险公司的赔偿。因为他不购买保险的预期效用为: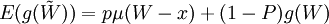 ,因此他购买保险的预期效用为μ(W − π),其中W − π就是他购买保险后的确定性收入。我们也可以计算得出,他的预期损失为utf − 8。如果保险费等于他的预期损失(这显然具有合理性),则π = W − E(W − px) = px,则购买保险后的确定收人
,因此他购买保险的预期效用为μ(W − π),其中W − π就是他购买保险后的确定性收入。我们也可以计算得出,他的预期损失为utf − 8。如果保险费等于他的预期损失(这显然具有合理性),则π = W − E(W − px) = px,则购买保险后的确定收人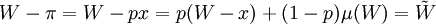 ,即保险所保证的稳定收入等于无保险情况下的财富收入的预期值。
,即保险所保证的稳定收入等于无保险情况下的财富收入的预期值。
由上面的分析得到,保险公司向个人销售保险的预期收入为零所确定的保险费与购买保险者要求保险费要等于预期损失是一致的,因此也是科学的。
假定他是一个风险厌恶者,其效用函数是严格凹的,这时有,
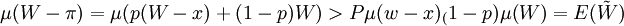
此式表明,购买保险的预期费用大于收入的预期效用,因此,购买保险对他来说是有利的,因此风险厌恶者愿意购买各种各样的保险。
下面我们解方程:
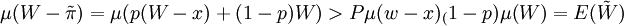
以此来求出他愿意支付的最高保险成本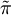 ,同时利用边际效用μ(w) > 0,即μ(w)严格单调递增,可知
,同时利用边际效用μ(w) > 0,即μ(w)严格单调递增,可知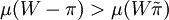 ,得出
,得出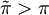 ,这说明最高保险费大于预期损失,此时作为理性人,他不会购买保险。同时,如果保险公司收取了较高的财产保险费,理性人会采取观望态度,保险公司的经营会受到影响。
,这说明最高保险费大于预期损失,此时作为理性人,他不会购买保险。同时,如果保险公司收取了较高的财产保险费,理性人会采取观望态度,保险公司的经营会受到影响。
下面我们讨论保险公司的经营状况。
鉴于保险公司向个人销售保险的预期收入为零,有人认为,这样保险公司不但不会赚钱,还要在经营中花掉管理费用、员工薪水等,保险公司就会亏本。事实并非如此。
事实上,保险公司作为经济人,也是以追求利润最大化为唯一目的。保险公司是投机者,只要他们有数量可观的保险单,他们就几乎没有什么风险。这可以由概率的大数定律来解释:虽然在一次实验中某事件发生的概率是随机的,但是在大量的重复独立实验中,该事件发生的频率却收敛于确定的常数。这样保险公司可以通过大面积操作来规避风险,达到盈利的目的。我们以人身保险为例说明。
某城镇每人每年的意外死亡率为0.006,若某人意外死亡,保险公司将赔付被保险人100000元,保险费为600元。假设有10000人购买此保险。则公司利润为:
10000×600-死亡人数×100000=(60-死亡人数)×100000.
每人每年死亡可看成是进行10000次重复独立的试验,即贝努里试验,设ζ表示10000人中意外死亡人数,则ζ~b(10000,0.006)即。
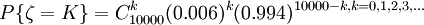
公司亏本的可能性,即为
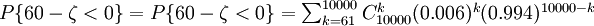 ,
,
利用De Moire-Laplace积分极限定理:
P{公司亏本}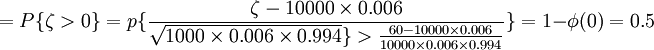
由于意外死亡发生的概率很小,每人对意外死亡规避度很高,保险公司并不用担心亏本的可能性只有0.5。
一般来说,保险公司会收取较高意外死亡保险费,并不影响该公司的业务。例如,保险费定为800元, 这时,P{公司亏本}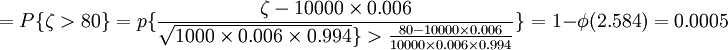
所以,保险公司几乎不会亏本。
效用函数的具体形式很多,比如完全替代效用函数、线性效用函数等等,本文只介绍了效用函数的幂函数形式和指数函数形式,因为金融学中这2种形式比较常用。在日常生活中,消费者都在有意无意地利用着效用函数进行消费,无论他们是否知道效用函数的具体形式。效用函数已经成为用数学方法研究经济问题的铺路石,通过对效用函数的数理分析,使经济学和金融学更有逻辑性。在解决实际问题中,我们可以根据一些具体条件和约束条件,建立最优化模型。根据对其效用函数性质的讨论,我们可以得到该模型唯一的最优解,而不用效用函数形式的不唯一性。
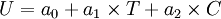 ;
;








该条目非常好,对于初学者而言,很有意义。