效用函数中的货币模型
出自 MBA智库百科(https://wiki.mbalib.com/)
效用函数中的货币模型(Money in the utility Function或MIU Model)
目录 |
效用函数中的货币模型由塞朝斯基(Sidrauski,1967)首先提出,模型假定行为人的效用既来自于对物品的消费也来自于对货币的持有。持有货币能够直接带来效用的原因在于货币的使用在“需求双向不吻合(No Double Coincidence of Wants)”的交易中减少了购物时间,而时间是能够为人们带来效用的。但要增加货币持有量就必须减少行为人的消费量或债券拥有量,而这些同样会为行为人带来效用。因此,行为人要使其效用极大化,需要在货币持有量与其消费量或债券拥有量之间进行权衡。如果稳态下模型经济的货币需求为正,它能为人们带来效用,那么,货币就具有了正的价值。MIU模型是首次在均衡分析中使货币真正具有正价值的模型。
效用函数中的货币模型的内容
效用函数中的货币模型将代表性行为人的效用函数表示为:
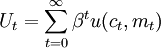 (1)
(1)
其中,ct( = C / N)为时期t人均消费,mt( = M / PN)为人均实际货币余额,0 < β < 1为贴现因子。通常假定uc > 0,um > 0,u(c,m)为严格凹函数。假定经济中有货币和物质资本2种资产,给定收入,行为人的财富分解为消费、资本投资和货币余额3部分。用τt 表示行为人在t期从政府那里得到的净转移支付,πt 表示通货膨胀率,Yt表示t期产量,δ表示资本折旧率,总体经济的预算限制可表示为:
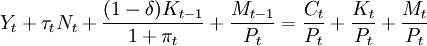 (2)
(2)
当人口增长率为n时,用人均量表示,等式(2)成为:
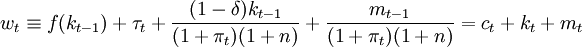 (3)
(3)
式中,f(kt − 1) = yt。
家庭在等式(3)的约束下选择ct ,kt和mt 使目标函数(1)极大化。对这一问题的分析可以 通过值函数进行。家庭初始财富wt是该问题的状态变量。令值函数V(wt)为家庭最优地选定消费、资本存量和货币余额时的效用现值:
其中,λ 是时期t消费的边际效用。根据包络定理有
λt = Vw(wt) = uc(ut,mt) (8)
一阶条件的含义为:初始条件分为消费、资本和货币余额3部分,在最佳配置下,各部分的边际效用相同。利用等式(5)和等式(8),等式(6)可写作:
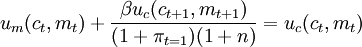 (9)
(9)
即在t期增加货币余额的边际收益等于该期消费的边际效用。
等式(5)一(7)与限制式(3)构成的体系描述了每一时点行为人选择的消费、资本量和货币余额,可以利用这一体系对经济动态进行分析。例如,通过对稳态的分析,可以等式(5)-(7)与限制式(3)构成的体系描述了每一时点行为人选择的消费、资本量和货币余额,可以利用这一体系对经济动态进行分析。例如,通过对稳态的分析,可以得出长期中资本存量独立于货币增长率、均衡时的消费水平与货币增长无关的货币超中性结论(Sidrausky,1967)。由于货币产生效用,通胀在减少货币余额时会带来福利损失,从而可以找出最优通胀率,它发生在名义利率为零时,这就是弗里德曼准则。对效用函数加以特殊设定,可以利用这一体系考察一国通货膨胀的福利成本(Lucas,1994)。
MIU模型开创了从行为人追求效用极大化来推导货币需求问题的先河,得出了在均衡状态下货币需求为正的结论。然而,该模型的假设前提是,货币的使用能减少购物时间,却没有直接去模拟为什么没有货币时交换就会困难。此外,该模型中隐含地假定货币是唯一的交换媒介,但模型中并没有任何明确的限制条件来达到这一目的。事实上,由于货币的回报率最低,人们完全可以以非货币形式持有财富,而只是在交换时才将一部分非金融资产换成货币。如果是这样,人们最优的决策就是将所有储蓄都放在生产资本或债券上,而不放在货币上。如果所有人都这么做,那么货币的需求只在一瞬间为正,而其他时候均为零。